a8-2a4+a2-2a+2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 7 2021
a) Ta có: \(\dfrac{m^2+2m+1}{m^2-1}\)
\(=\dfrac{\left(m+1\right)^2}{\left(m+1\right)\left(m-1\right)}\)
\(=\dfrac{m+1}{m-1}\)
b) Ta có: \(\dfrac{2a^4+3a^3+2a+3}{\left(a^2-a+1\right)\left(4a+6\right)}\)
\(=\dfrac{a^3\left(2a+3\right)+\left(2a+3\right)}{\left(a^2-a+1\right)\left(4a+6\right)}\)
\(=\dfrac{\left(2a+1\right)\left(a+1\right)\left(a^2-a+1\right)}{2\left(a^2-a+1\right)\left(2a+3\right)}\)
\(=\dfrac{a+1}{2}\)
DT
0
MV
10 tháng 8 2017
Áp dụng tính chất DTSBN:
\(\dfrac{a_1}{a_2}=\dfrac{a_2}{a_3}=...=\dfrac{a_9}{a_1}=\dfrac{a_1+a_2+...+a_9}{a_2+a_3+...+a_1}=1\)
\(\dfrac{a_1}{a_2}=1\Rightarrow a_1=a_2\)
\(\dfrac{a_2}{a_3}=1\Rightarrow a_2=a_3\)
...
\(\dfrac{a_9}{a_1}=1\Rightarrow a_9=a_1\)
\(\Rightarrow a_1=a_2=...=a_9\)
DT
0
NT
0
DQ
1
18 tháng 12 2016
\(\frac{a_1}{a_2}=\frac{a_2}{a_3}=.......=\frac{a_9}{a_1}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a_1}{a_2}=\frac{a_2}{a_3}=.......=\frac{a_9}{a_1}=\frac{a_1+a_2+.......+a_9}{a_2+a_3+......+a_1}=1\)
=> a1 = a2
a2 = a3
a3 = a4
.........
=> a1 = a2 = a3 = ...... = a9
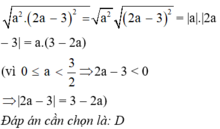
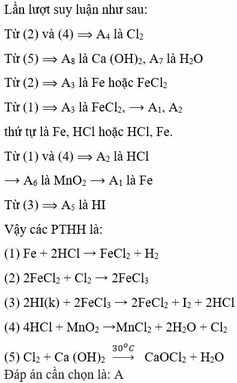
\(\Leftrightarrow a^8-a^6+a^6-a^4-a^4+a^2-2a+2=0\)
\(\Leftrightarrow a^6\left(a^2-1\right)+a^4\left(a^2-1\right)-a^2\left(a^2-1\right)-2\left(a-1\right)=0\)
\(\Leftrightarrow\left(a^6+a^4-a^2\right)\left(a-1\right)\left(a+1\right)-2\left(a-1\right)=0\)
\(\Leftrightarrow a=1\)