cho 2 điểm A,B cố định và phân biệt , đường tròn (I) đường kính AB . Điểm M trên (I) , M khác A,B , tia MI cắt (I) tại N , tiếp tuyến tại B với (I) cắt AM , AN lần lượt tại P,Q . Chứng minh khi điểm M đi chuyển trên đường tròn (I) thì trực tâm H của tam giác MPQ đi chuyển trên một đường cố định , xác định đường cố định ấy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1
Sửa đề: M,N,P,Q cùng thuộc một đường tròn
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>BM\(\perp\)AQ tại M
Xét (O) có
ΔBNA nội tiếp
BA là đường kính
Do đó: ΔBNA vuông tại N
=>BN\(\perp\)AP
Xét ΔABQ vuông tại B có BM là đường cao
nên \(AM\cdot AQ=AB^2\left(1\right)\)
Xét ΔABP vuông tại B có BN là đường cao
nên \(AN\cdot AP=AB^2\left(2\right)\)
Từ (1),(2) suy ra \(AM\cdot AQ=AN\cdot AP\)
=>\(\dfrac{AM}{AP}=\dfrac{AN}{AQ}\)
Xét ΔAMN và ΔAPQ có
\(\dfrac{AM}{AP}=\dfrac{AN}{AQ}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN đồng dạng với ΔAPQ
=>\(\widehat{AMN}=\widehat{APQ}\)
mà \(\widehat{AMN}+\widehat{QMN}=180^0\)(hai góc kề bù)
nên \(\widehat{QMN}+\widehat{QPN}=180^0\)
=>MNPQ là tứ giác nội tiếp
=>M,N,P,Q cùng thuộc một đường tròn
11 tháng 11 2021
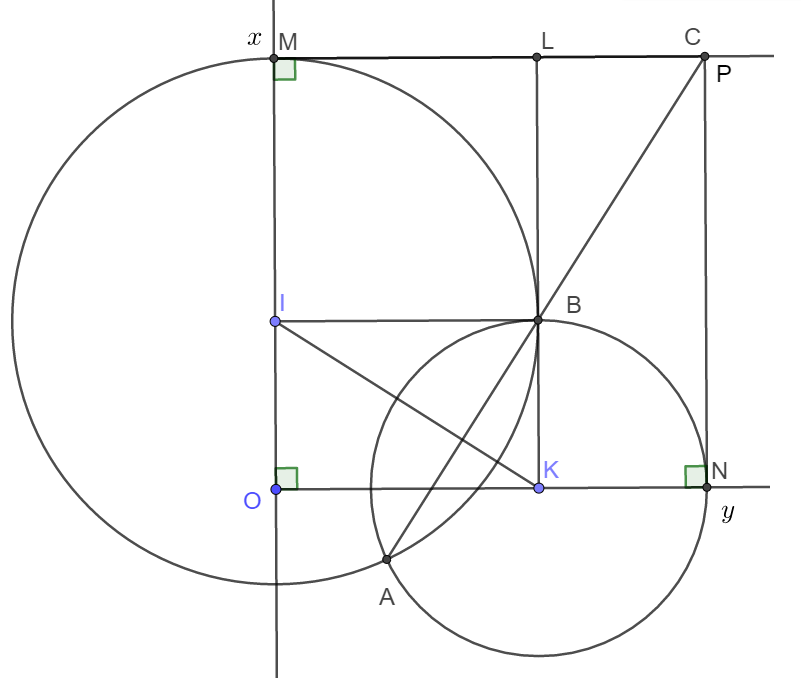
a) Trong tam giác OIK có:
|OK OI| < IK < |OK + OI| hay .
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra . Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.
CM
15 tháng 3 2018
a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C
6 tháng 1 2023
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đo: ΔACB vuông tại C
Xét (O) co
ΔADB nội tiếp
ABlà đườg kính
Do đó:ΔADB vuông tại D
AC*AM=AB^2
AD*AN=AB^2
=>AC*AM=AD*AN
b: Xét ΔOBI và ΔOCI có
OB=OC
IB=IC
OI chung
Do đó:ΔOBI=ΔOCI
=>góc OCI=90 độ
=>IC là tiếp tuyến của (O)
CM
3 tháng 11 2018
a, Chú ý: A M O ^ = A I O ^ = A N O ^ = 90 0
b, A M B ^ = M C B ^ = 1 2 s đ M B ⏜
=> DAMB ~ DACM (g.g)
=> Đpcm
c, AMIN nội tiếp => A M N ^ = A I N ^
BE//AM => A M N ^ = B E N ^
=> B E N ^ = A I N ^ => Tứ giác BEIN nội tiếp => B I E ^ = B N M ^
Chứng minh được: B I E ^ = B C M ^ => IE//CM
d, G là trọng tâm DMBC Þ G Î MI
Gọi K là trung điểm AO Þ MK = IK = 1 2 AO
Từ G kẻ GG'//IK (G' Î MK)
=> G G ' I K = M G M I = M G ' M K = 2 3 I K = 1 3 A O không đổi (1)
MG' = 2 3 MK => G' cố định (2). Từ (1) và (2) có G thuộc (G'; 1 3 AO)
13 tháng 1 2017
(Quá lực!!!)
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)