(2 điểm) Một người đi xe đạp trên một đoạn đường dài 1,2 km hết 6 phút. Sau đó người đó đi tiếp một đoạn đường 0,6 km trong 4 phút rồi dừng lại. Tính tốc độ trung bình của người đó ứng với từng đoạn đường và cả đoạn đường.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vận tốc trung bình bằng tổng quãng đường chia cho tổng thời gian đi hết quãng đường đó.
Quãng đường người đi xe đạp đã đi là: S = 1,2 + 0,6 = 1,8 (km)
Thời gian người đó đi là: t = 6 + 4 = 10 (phút) = 1/6 (h)
Vận tốc trung bình: \(v=\dfrac{S}{t}=1,8:\dfrac{1}{6}=10,8\) (km/h)

bạn lưu ý đây là lí chứ ko phải hóa nhé!
*sao nhiều người hay nhầm cái khái niệm thế nhỉ*
tóm tắt
\(s_1=1,2km=1200m\)
\(t_1=6min\)
\(s_2=0,6km=600m\)
\(t_2=4min\)
\(v_{tb}=?\)
giải
ADCT \(v=\dfrac{s}{t}\) ta có:
vận tốc của người đi xe đạp trên quãng đường thứ nhất là:
\(\dfrac{1200}{6}=200m\)/\(min\)
vận tốc của người đi xe đạp trên quãng đường thứ hai là:
\(\dfrac{600}{4}=150m\)/\(min\)
ADCT \(v_{tb}=\dfrac{s}{t}\); ta có:
vận tốc trung bình của người đi xe đạp trên cả 2 đoạn đường là:
\(v_{tb}=\dfrac{1200+600}{6+4}=180m\)/\(min\)
vậy vận tốc trung bình của người đi xe đạp trên cả 2 đoạn đường là \(180m\)/\(min\)

Đổi: \(6ph=\dfrac{1}{10}h,4ph=\dfrac{1}{15}h\)
\(\left\{{}\begin{matrix}v_1=\dfrac{S_1}{t_1}=\dfrac{1,2}{\dfrac{1}{10}}12\left(km/h\right)\\v_2=\dfrac{S_2}{t_2}=\dfrac{0,6}{\dfrac{1}{15}}=9\left(km/h\right)\\v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{1,2+0,6}{\dfrac{1}{10}+\dfrac{1}{15}}=10,8\left(km/h\right)\end{matrix}\right.\)
Tóm tắt:
\(S_1=1,2km\), \(S_2=0,6km\)
\(t_1=6\text{phút}=0,1\text{giờ}\), \(t_2=4\text{phút}=\dfrac{1}{15}\text{giờ}\)
\(v_1=?\text{km/h},v_2=?\text{km/h},v_{tb}=?\text{km/h}\)
Giải:
Vận tốc trung bình khi đạp xe: \(v_1=\dfrac{S_1}{t_1}=\dfrac{1,2}{0,1}=12\text{(km/h)}\)
Vận tốc trung bình khi đi bộ: \(v_2=\dfrac{S_2}{t_2}=0,6\div\dfrac{1}{15}=9\text{(km/h)}\)
Vận tốc trung bình khi đi cả đoạn đường: \(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{1,2+0,6}{0,1+\dfrac{1}{15}}=10,8\text{(km/h)}\)

S1 = 1,2 km
t1 = 6 phút = 0,1 giờ
S2 = 0,6 km
t2 = 4 phút = \(\frac{1}{15}\) giờ.
vtb = ?
Giải:
Vận tốc trung bình trên cả quãng đường là:
Vtb = \(\frac{S_1+S_2}{t_1+t_2}=\frac{1,2+0,6}{\frac{1}{10}+\frac{1}{15}}=10,8\) (km/h)

12 phút = 0,2 giờ
3 phút = 0,05 (giờ)
Vận tốc trung bình trên đoạn đầu là:
5,2 : 0,2 = 26 (km/h)
Vận tốc trung bình trên đoạn sau :
1,2 : 0,05 = 24 (km/h)
Vận tốc trung bình trên cả đoạn đường :
( 5,2 + 1,2) : ( 0,2 + 0,05) = 25,6 (km/h)
Kết luận :...

Vận tốc của người đó trên quãng đường 1 là
\(v=\dfrac{s}{t}=1,8:0,15=12\left(kmh\right)\)
Vận tốc của người đó trên quãng đường 2 là
\(v=\dfrac{s}{t}=2,7:0,25=10,8\left(kmh\right)\)
Vận tốc trung bình của người đó trên cả 2 quãng đường là
\(v_{tb}=\dfrac{s+s'}{t+t'}=\dfrac{1,8+2,7}{0,25+0,15}=\dfrac{4,5}{0,4}=11,25\left(kmh\right)\)
=> Chọn B

(3,0 điểm)
Tóm tắt: (0,5 điểm)
s 1 = 300m; t 1 = 2 phút = 120 s
s 2 = 500m; t 2 = 2,5 phút = 150 s
Tính: v tb = ?
Giải
Vận tốc trung bình của người đi xe đạp trên cả hai quãng đường là: (0,5 điểm)
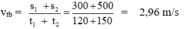 (0,5 điểm)
(0,5 điểm)

bai toan thiếu dữ kiên khong the lam dc,cần phải có 1 tr0ng các du kien sau;
1. thoi gian xe chay voi 8km/h
2. quang dg co chieu dai la......
3. tong t xe chay
Đổi : \(6p=\dfrac{6}{60}h=\dfrac{1}{10}h;4p=\dfrac{4}{60}h=\dfrac{1}{15}h\)
\(v_1=\dfrac{S_1}{t_1}=\dfrac{1,2}{\dfrac{1}{10}}=12\left(km/h\right)\)
\(v_2=\dfrac{S_2}{t_2}=\dfrac{0,6}{\dfrac{1}{15}}=9\left(km/h\right)\)
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{1,2+0,6}{\dfrac{1}{10}+\dfrac{1}{15}}=10,8\left(km/h\right)\)
Tóm tắt:
s_1=1,2s1=1,2 km
t_1=6t1=6 phút =\dfrac{1}{10}=101 h
s_2=1,6s2=1,6 km
t_2=4t2=4 phút =\dfrac{1}{15}=151 h
v_1,v_{2,}v_{tb}=?v1,v2,vtb=?
Bài làm:
Tốc độ của người đó trên đoạn đường đầu tiên là:
v_1=\dfrac{s_1}{t_1}=12v1=t1s1=12 (km/h)
Tốc độ của người đó trên đoạn đường sau là:
v_2=\dfrac{s_2}{t_2}=9v2=t2s2=9 (km/h)
Tốc độ trung bình của người đó trên cả hai đoạn đường là:
v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=10,8vtb=t1+t2s1+s2=10,8 (km/h)