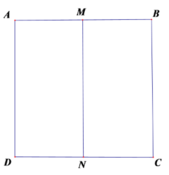
ABCD là 1 hình vuông. Gọi trung điểm cua AB, CD lần lượt là M và N. Khi đó diện tích hình vuông ABCD là ... \(cm^2\)?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có : \(S_{ABCD}=36cm^2\Rightarrow BC^2=36\Rightarrow BC=6cm\left(Vi:BC>0\right)\)
Vì ABCD là hình vuông (gt)
\(\Rightarrow BC=DC=AD=AB=6\left(cm\right)\)
Mà : M , N lần lượt là trung điểm của BC , CD
\(\Rightarrow BM=MC=DN=NC=\frac{BC}{2}=\frac{6}{2}=3\left(cm\right)\)
Có : \(S_{AMN}=S_{ABCD}-\left(S_{ADN}+S_{ABM}+S_{NMC}\right)\)
\(=36-\left(\frac{1}{2}.AD.DN+\frac{1}{2}.AB.BM+\frac{1}{2}.MC.NC\right)\)
\(=36-\left(\frac{1}{2}.6.3+\frac{1}{2}.6.3+\frac{1}{2}.3.3\right)=\frac{27}{2}\left(cm^2\right)\)
Chúc bạn học tốt !!!

Mặt trụ tạo bởi hình vuông ABCD khi quay quanh MN có đường cao h = a và bán kính đáy ![]()
Diện tích 1 đáy và diện tích xung quanh của hình trụ là:
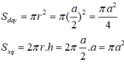
Nên có diện tích toàn phần của hình trụ:
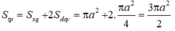
Mặt cầu (S) có bán kính R có diện tích bằng Stp của mặt trụ nên:
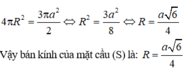

a: Xét ΔABD có
M là tđiểm của AB
Q là tđiểm của AD
Do đó:MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là tđiểm của BC
P là tđiểm của CD
Do đó: NP là đường trung bình
=>NP=BD/2 và NP//BD(2)
Xét ΔABC có
M là tđiểm của AB
N là tđiểm của BC
Do đó: MN là đường trung bình
=>MN=AC/2=BD/2(3)
Từ (1) và (3) suy ra MN=MQ
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành
mà MN=MQ
nên MQPN là hình thoi

a) MN là đường trung bình tam giác HDC \(\Rightarrow\hept{\begin{cases}MN=\frac{1}{2}DC=AB\\MN//DC//AB\end{cases}}\)=> MNAB là hình bình hành
b) Có \(\hept{\begin{cases}MN//DC\\AD\perp DC\end{cases}\Rightarrow MN\perp AD}\)
Mà \(DN\perp AM\)nên N là trực tâm tam giác AMD \(\Rightarrow AN\perp DM\)
Mà \(BM//AN\)(vì ANMB là hình bình hành) nên \(BM\perp DM\Rightarrow\widehat{BMD}=90^0\)
c) \(S_{ABCD}=\frac{\left(AB+DC\right).AD}{2}=\frac{\left(\frac{DC}{2}+DC\right).AD}{2}=\frac{\left(8+16\right).6}{2}=72\left(cm^2\right)\)

a, có M;N lần lượt là trđ của HC; HD (gt) xét tg DHC
=> MN là đtb của tg DHC (đn)
=> MN // DC mà DC // AB (do ABCD là hình thang) => AB // MN
MN = 1/2DC (tc) mà DC = 2AB => AB = 1/2DC => MN = AB
=> ABMN là hình bình hành (dấu hiệu)
b, MN // DC (câu a) DC _|_ AD (gt)
=> MN _|_ AD ; DN _|_ AM (gt) ; xét tg DAM
=> N là trực tâm của tg DAM
=> AN _|_ DM mà AN // BM do ABMN là hình bình hành (câu a)
=> DM _|_ BM (TC)
=> ^BMD = 90
c, có CD thì tính đc AB xong tính bth

- Đề sai nha bạn :)