tính giá trị biểu thức 0,04x 0,8x 1,25x 2x 25x 1000+ 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x=24 nên x+1=25
C=x^4-x^3(x+1)+x^2(x+1)-x(x+1)+30
=x^4-x^4-x^3+x^3+x^2-x^2-x+30
=-x+30
=30-24
=6

1) \(4-25x^2=0\)
\(\Rightarrow\left(2-5x\right)\left(2+5x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}5x=2\\5x=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{5}\\x=-\dfrac{2}{5}\end{matrix}\right.\)
2) Tính thì phải cho giá trị của x.
\(A=x^3-3x^2+3x-1\)
\(=\left(x-1\right)^3\)
\(=\left[{}\begin{matrix}\left(\dfrac{5}{2}-1\right)^3=\dfrac{27}{8}\\\left(-\dfrac{5}{2}-1\right)^3=-\dfrac{343}{8}\end{matrix}\right.\)

Câu 2:
a: ĐKXĐ: \(x\notin\left\{0;2\right\}\)
b: Sửa đề: \(A=\left(\dfrac{2x-x^2}{2x^2+8}-\dfrac{2x^2}{x^3-2x^2+4x-8}\right)\cdot\left(\dfrac{2}{x^2}-\dfrac{x-1}{x}\right)\)
\(=\left(\dfrac{2x-x^2}{2\left(x^2+4\right)}-\dfrac{2x^2}{\left(x-2\right)\left(x^2+4\right)}\right)\cdot\dfrac{2-x\left(x-1\right)}{x^2}\)
\(=\left(\dfrac{\left(2x-x^2\right)\left(x-2\right)-4x^2}{2\left(x^2+4\right)\left(x-2\right)}\right)\cdot\dfrac{2-x^2+x}{x^2}\)
\(=\dfrac{\left(x^2-2x\right)\left(x-2\right)+4x^2}{2\left(x^2+4\right)\left(x-2\right)}\cdot\dfrac{x^2-x-2}{x^2}\)
\(=\dfrac{x^3-2x^2-2x^2+4x+4x^2}{2\left(x^2+4\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)\left(x+1\right)}{x^2}\)
\(=\dfrac{x^3+4x}{2\left(x^2+4\right)}\cdot\dfrac{x+1}{x^2}\)
\(=\dfrac{x\left(x^2+4\right)\left(x+1\right)}{2\left(x^2+4\right)\cdot x^2}=\dfrac{x+1}{2x}\)
c: Khi x=2024 thì \(A=\dfrac{2024+1}{2\cdot2024}=\dfrac{2025}{4048}\)
Câu 1:
a: \(25x^2\left(x-3y\right)-15\left(3y-x\right)\)
\(=25x^2\left(x-3y\right)+15\left(x-3y\right)\)
\(=\left(x-3y\right)\left(25x^2+15\right)\)
\(=\left(x-3y\right)\cdot5\cdot\left(5x^2+3\right)\)
b: \(x^4-5x^2+4\)
\(=x^4-x^2-4x^2+4\)
\(=\left(x^4-x^2\right)-\left(4x^2-4\right)\)
\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left(x^2-4\right)=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)

\(C=\sqrt{25x^2-20x+4}+\sqrt{25x^2}\)
\(C=\sqrt{\left(5x-2\right)^2}+\sqrt{\left(5x\right)^2}\)
\(C=\left|5x-2\right|+\left|5x\right|=\left|2-5x\right|+\left|5x\right|\)
\(C\ge\left|2-5x+5x\right|=2\)
Dấu " = " xảy ra \(\Leftrightarrow\)( 2 - 5x ) . 5x \(\ge\)0
\(\Leftrightarrow\)\(\hept{\begin{cases}x\ge0\\2-5x\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}x\le0\\2-5x\le0\end{cases}}\)
\(\Leftrightarrow\)\(0\le x\le\frac{2}{5}\)
Vậy GTNN của C là 2 \(\Leftrightarrow\)\(0\le x\le\frac{2}{5}\)
\(C=\sqrt{25x^2-20x+4}+\sqrt{25x^2}\)
\(C=\sqrt{\left(5x-2\right)^2}+\sqrt{\left(5x\right)^2}\)
\(C=\left|5x-2\right|+\left|5x\right|\)
\(C=\left|2-5x\right|+\left|5x\right|\ge\left|2-5x+5x\right|=2\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}2-5x\ge0\\5x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le\frac{2}{5}\\x\ge0\end{cases}\Leftrightarrow0\le}x\le\frac{2}{5}}\)


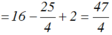
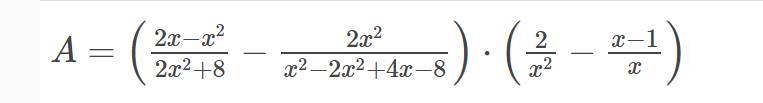
Kết quả là 2004 chắc chắn 100% luôn.
tinh ket qua 0,04 x 0,8 x1,25x 2x1000 roi cong 4