cho hình vuông abcd có cạnh là 12 cm trên đường chéo BD lấy điểm M và N sao cho BM=MN=ND tính diện tích tứ giác AMCN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta thấy các hình tam giác nhỏ bằng nhau thì ta lấy diện tích hình vuông chia cho 6 nhân 2 là ra diện tích hình tứ giác AMCN

Theo đầu bài ta có hình sau:
A B C D M N 6,6 cm
Ta có: \(S_{ABCD}=6,6\cdot6,6=43,56\left(cm^2\right)\)
Ta thấy: \(\hept{\begin{cases}DM=MN=NB\\DM+MN+NB=DB\end{cases}}\)
\(\Rightarrow MN=\frac{1}{3}DB\)
\(\Rightarrow\hept{\begin{cases}S_{AMN}=\frac{1}{3}S_{ADB}\\S_{CMN}=\frac{1}{3}S_{CDB}\end{cases}}\)
\(\Rightarrow S_{AMN}+S_{CMN}=\frac{1}{3}S_{ADB}+\frac{1}{3}S_{CDB}\)
\(\Rightarrow S_{AMN}+S_{CMN}=\frac{1}{3}\left(S_{ADB}+S_{CDB}\right)\)
\(\Rightarrow S_{AMCN}=\frac{1}{3}S_{ABCD}\)
\(\Rightarrow S_{AMCN}=\frac{1}{3}\cdot43,56\)
\(\Rightarrow S_{AMCN}=14,52\left(cm^2\right)\)
Vậy diện tích hình tứ giác AMCN là 14,52 cm2.

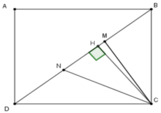
Ta có CD = AB = 9cm; BC = AD = 8cm nên SBCD = 1 2 BC.DC = 1 2 .8.9 = 36cm2
Kẻ CH ⊥ BD tại H
Ta có: SBCD = 1 2 CH.BD; SCMN = 1 2 CH.MN mà MN = 1 3 BD
=> SCMN = 1 3 SBCD = 1 3 .36 = 12cm2
Đáp án cần chọn là: A

S ABCD là: 6,6 x 6,6= 43,56(m2)
DM=MN=NB và bằng: 6,6:3= 2,2(m)
S ABN: 6,6 X 2,2 :2 = 7,26(M)
S AMD: 6,6 X 2,2 :2 = 7,26(M)
S MDC: 6,6 X 2,2 :2 = 7,26(M)
S BCN 6,6 X 2,2 :2= 7,26(M)
A AMCN: 43,56 - 7,26 X 4 = 14,52(M)
ĐS: 14,52M HỌC TỐT

Cách 1 : ét tam giác ADM và tam giác CDM, ta có:
DM chung
AD=DC( tg ABCD là hình vuông)
Ta có: ABCD là hình vuông => BD là tia phân giác của góc B do đó góc ADM = góc CDM
=> tam giác ADM = tam giác CDM ( c-g-c )
=> AM = MC (1)
Chứng minh tương tự ta có: tam giác ABN = tam giác CBN ( c-g-c )
Do đó AN = NC (2)
Xét tam giác ADM và tam giác ABN, ta có:
DM=NB (gt)
AD=AB (gt)
góc ADM = góc ABN (gt)
=> tam giác ADM = tam giác ABN ( c-g-c)
do đó: AM = AN (3)
Từ (1); (2) và (3) => tg AMCN là hình thoi
Xét tam giác ADB theo định lí pi-ta-go ta có:
DB^2 = AD^2 + AB^2= 6,6^2 + 6,6^2 =2178/25
DB= căn 2178/25 =33 căn2/5
Ta lại có DM=MN=NB
DM+MN+NB=DB
=> 3MN= DB => MN= DB: 3= 33 căn2 / 5 : 3= 11 căn 2 /5
Sabcd= 1/2(AC*MN)= 14,5 cm vuông
Cách 2 : Áp dụng định lí Py-ta-go vào tam giác vuông cân ABC ta có :
BD=√(AB^2+AD^2)=√(6,6^2+6,6^2)=33√(2):5 (cm)
=> MN = BD :3 = 33√(2) : 3 = 11√(2) : 5 (cm)
Ta có : Hai đường chéo của hình vuông vuông góc với nhau tại H
Vì AB=AD ; Góc DAC = 90 độ
=> Tam giác ADB vuông cân tại A
=> Góc ADB = Góc ABD = 90:2 = 45 (độ)
Vì AC = BD = 33√(2) : 5 cm
=> S(AMCN) = (MN.AC) : 2 = ((11√(2) : 5).(33√(2) : 5)):2 = 14,5 (cm^2)

Diện tích hình chữ nhật ABCD là:
8x9 =72 (cm^2)
S ABD= S BDC = 1/2 S ABCD
S CMN = 1/3 S BDC
Suy ra: S CMN = 1/6 S ABCD
Diện tích tam giác CMN là:
72 .1/6 =12 (cm^2)
S là kí hiệu của diện tích. Chúc bạn học tốt
ABCDMHN
Tứ giác AMCN có hai đường chéo AC và MN vuông góc với nhau tại trung điểm của mỗi đường.
Thật vậy ta có:
\(AC\perp BD\Rightarrow AC\perp MN\)
\(\left\{{}\begin{matrix}HA=HC\\HB=HD\end{matrix}\right.\) hai đường chéo hình vuông thì vuông góc tại trung điểm của mỗi đường.
\(HB=HD\Rightarrow DN+NH=BM+MH\Rightarrow NH=MH\)
Vậy tứ giác AMCN là hình thoi.
Diện tích hình thoi AMCN là:
\(S_{AMCN}=\dfrac{1}{2}AC.MN=\dfrac{1}{2}AC.BD.\dfrac{1}{3}\\ =S_{ABCD}.\dfrac{1}{3}=\dfrac{1}{3}.12.12=48cm^2\)
Đs....