giúp 2 câu này với:
1/Giải phương trình: (x2-20162)2-8064x-1
2/CM trong 4 số tn liên tiếp, tổng của lập phương ba số đầu bằng lập phương số thứ tư: n3+(n+1)3+(n+2)3=(n+3)3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
KN
10 tháng 3 2018
Gọi x là số thứ nhất (x<0)
số thứ hai là: x + 1
Số thứ ba là: x + 2
Số thứ tư là : x + 3
Do tổng lập phương 3 số đầu bằng lập phương số thứ tư nên ta có phương trính:
x3 + (x + 1)3 + (x + 2)3 = (x + 3)3
\(\Leftrightarrow\) x3 + x3 + 3x2 + 3x + 1 + x3 + 6x2 + 12x + 8 = x3 + 9x2 + 27x + 27
\(\Leftrightarrow\) 3x3 + 9x2 + 15x + 9 = x3 + 9x2 + 27x + 27
\(\Leftrightarrow\) 3x3 - x3 + 9x2 - 9x2 + 15x - 27x + 9 - 27 = 0
\(\Leftrightarrow\) 2x3 - 12x - 18 = 0
\(\Leftrightarrow\) 2x3 - 6x2 + 6x2 - 18x + 6x - 18 = 0
\(\Leftrightarrow\) 2x2(x - 3) + 6x(x - 3) + 6(x - 3) = 0
\(\Leftrightarrow\) 2(x2 + 3x + 3)(x - 3) = 0
vì x2 + 3x + 3 = \(\left(x+\dfrac{3}{2}\right)\)2 + \(\dfrac{3}{4}\) \(\ge\) \(\dfrac{3}{4}\) > 0
\(\Leftrightarrow\) x - 3 = 0
\(\Leftrightarrow\) x = 3 (tm)
Vậy 4 số cần tìm lần lượt là: 3;4;5;6
HP
24 tháng 1 2017
gọi 4 số tự nhiên đó lần lượt là a-2,a-1,a,a+1
ta có (a-2)3+(a-1)3+a3=(a+1)3
khai triển rồi rút gọn ta được 2a3-12a2+12a-10=0
<=>2a3-10a2-2a2+10a+2a-10=0
<=>2a2(a-5)-2a(a-5)+2(a-5)=0
<=>(a-5)(2a2-2a+2)=0
<=>(a-5)(a2-a+1)=0
<=>a-5=0<=>a=5 (vì a2-a+1=(a-1/2)2+3/4>0 với mọi a)
Vậy 4 số tự nhiên liên tiếp cần tìm là 3;4;5;6
13 tháng 7 2023
Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
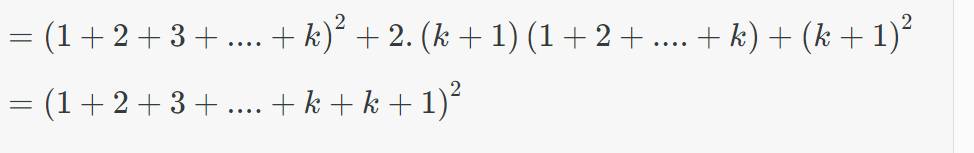
=>ĐPCM
3 tháng 2 2017
Vì vận tốc lúc đi lớn hơn lúc về 10km/h nên ta có phuong trình :
x/3+x/3,5=10
3,5x+3x/10,5=105/10,5
6,5x=105
x=16,2
Vậy quãng đường AB dài 16,2km
TT
14 tháng 8 2020
Đề bài : Chứng minh rằng tổng lập phương của các số tự nhiên liên tiếp từ 1 đến n bằng bình phương của tổng từ 1 đến n ( n tự nhiên ). Hay ta cần chứng minh : \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) (*)
Lời giải :
+) Xét \(n=1\) thì ta có : \(1^3=1^2\) ( đúng )
Suy ra (*) đúng với \(n=1\) (1)
+) Xét \(n=2\) ta có : \(1^3+2^3=1+8=9\); \(\left(1+2\right)^2=3^2=9\)
\(\Rightarrow1^3+2^3=\left(1+2\right)^2\) ( đúng ). Nên (*) đúng với \(n=2\) (2)
+) Giả sử (*) đúng với \(n=k\). Tức là : \(1^3+2^3+3^3+....+k^3=\left(1+2+...+k\right)^2\).
Ta cần chứng minh \(n=k+1\) cũng đúng với (*). Thật vậy , ta có :
\(1^3+2^3+3^3+.....+\left(k+1\right)^3\)
\(=1^3+2^3+....+k^3+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+\left(k+1\right)^3\)
Xét biểu thức \(\left(k+1\right)^2+2.\left(k+1\right).\left(1+2+3+....+k\right)\)
\(=\left(k+1\right)^2+2.\left(k+1\right)\cdot\frac{\left(k+1\right).k}{2}\)
\(=\left(k+1\right)^2+\left(k+1\right)^2.k=\left(k+1\right)^3\)
Do đó \(1^3+2^3+....+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+2.\left(k+1\right)\left(1+2+....+k\right)+\left(k+1\right)^2\)
\(=\left(1+2+3+....+k+k+1\right)^2\)
Vậy (*) đúng với \(n=k+1\) (3)
Từ (1) (2) và (3) suy ra \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) với mọi \(n\in N\).
6 tháng 10 2021
a) Từ giả thiếtta có thể đặt : \(n^2-1=3m\left(m+1\right)\) với m là 1 số nguyên dương
Biến đổi phương trình ta có :
\(\left(2n-1;2n+1\right)=1\) nên dẫn đến :
\(TH1:2n-1=3u^2;2n+1=v^2\)
\(TH2:2n-1=u^2;2n+1=3v^2\)
\(TH1:\)
\(\Rightarrow v^2-3u^2=2\)
\(\Rightarrow v^2=2\left(mod3\right)\)
Còn lại TH2 cho ta \(2n-1\) là số chính phương
b) Ta có :
\(\frac{n^2-1}{3}=k\left(k+1\right)\left(k\in N\right)\)
\(\Leftrightarrow n^2=3k^2+3k+1\)
\(\Leftrightarrow4n^2-1=12k^2+12k+3\)
\(\Leftrightarrow\left(2n-1\right)\left(2n+1\right)=3\left(2k+1\right)^2\)
- Xét 2 trường hợp :
\(TH1:\Rightarrow\hept{\begin{cases}2n-1=3p^2\\2n+1=3q\end{cases}}\)
\(TH2:\Rightarrow\hept{\begin{cases}2n-1=p^2\\2n+1=3q^2\end{cases}}\)
+) TH1 :
Hệ \(PT\Leftrightarrow q^2=3p^2+2=2\left(mod3\right)\) ( loại, vì số chính phương chia 3 dư 0 hoặc 1 )
+) TH2 :
Hệ \(PT\Leftrightarrow p=2a+1\Rightarrow2n=\left(2a+1\right)^2+1\Rightarrow n^2=a^2+\left(a+1\right)^2\) ( dpcm )