Tính số đo góc tạo bởi đt (d) . PT : \(y=\dfrac{-\sqrt{3}}{3}x+1\) với tia Ox
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Gọi \(M\left(x;y\right)\) là điểm bất kì nằm trên phân giác
\(\Rightarrow d\left(M;d_1\right)=d\left(M;d_2\right)\Leftrightarrow\dfrac{\left|3x-4y-3\right|}{\sqrt{3^2+\left(-4\right)^2}}=\dfrac{\left|12x+5y-12\right|}{\sqrt{12^2+5^2}}\)
\(\Leftrightarrow\left|39x-52y-39\right|=\left|60x+25y-60\right|\)
\(\Rightarrow\left[{}\begin{matrix}60x+25y-60=39x-52y-39\\60x+25y-60=-39x+52y+39\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+11y-3=0\\11x-3y-11=0\end{matrix}\right.\)
Xét \(3x+11y-3=0\) có vtpt \(\left(3;11\right)\)
Ta có: \(cos^{-1}\dfrac{\left|3.3-11.4\right|}{\sqrt{3^2+\left(-4\right)^2}.\sqrt{3^2+11^2}}=52^0>45^0\) (ktm)
\(\Rightarrow11x-3y-11=0\) là pt đường phân giác góc nhọn tạo bởi d1 và d2
2.
Phương trình d1: \(\sqrt{2}x-\sqrt{2}y+2m=0\)
Đường tròn (C) có tâm \(O\left(0;0\right)\) bán kính \(R=1\)
Đường thẳng d1 tiếp xúc với (C) khi và chỉ khi:
\(d\left(O;d_1\right)=R\)
\(\Leftrightarrow\dfrac{\left|2m\right|}{\sqrt{2+2}}=1\Leftrightarrow\left|2m\right|=2\)
\(\Rightarrow m=\pm1\)

\(a,\Leftrightarrow3m-1=-2\Leftrightarrow m=-\dfrac{1}{3}\Leftrightarrow\left(d\right):y=-\dfrac{1}{3}x-1\\ c,\text{Hs góc: }-\dfrac{1}{3}\\ \text{Gọi góc cần tìm là }\alpha>90^0\\ \Leftrightarrow\tan\left(180^0-\alpha\right)=\dfrac{1}{3}\approx\tan18^0\\ \Leftrightarrow\alpha\approx180^0-18^0=162^0\)

a/ \(k=-1=tan\alpha\Rightarrow\alpha=135^0\)
b/ Phương trình d: \(y=kx+b\)
\(\Rightarrow\left\{{}\begin{matrix}0.k+b=1\\k.\left(-\sqrt{3}\right)+b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=1\\k=\frac{1}{\sqrt{3}}\end{matrix}\right.\)
\(\Rightarrow tan\alpha=k=\frac{1}{\sqrt{3}}\Rightarrow\alpha=30^0\)

a) Đồ thị như hình bên.
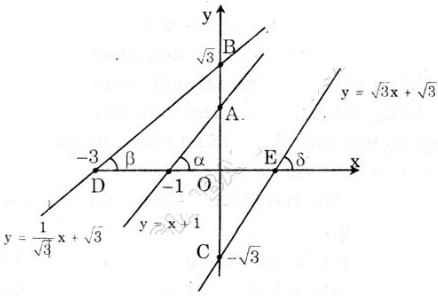
b) tgα = 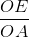 = 1,
= 1,
tgβ = 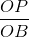 =
= 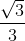 =
= 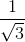 ,
,
tgɣ = 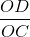 =
= 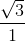 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .
a) Đồ thị như hình bên.

b) tgα = 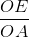 = 1,
= 1,
tgβ = 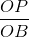 =
= 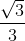 =
= 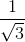 ,
,
tgɣ = 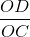 =
= 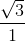 = √3.
= √3.
Suy ra α = 450, β = 300, ɣ = 600 .

Lời giải:
a.
Đồ thị màu xanh lá: $y=\frac{1}{2}x+1$
Đồ thị màu xanh dương: $y=-x-1$
b.
Ta có:
$\tan \alpha=\frac{1}{2}\Rightarrow \alpha=26,57^0$
$\tan \beta = -1\Rightarrow \beta=135^0$

d nhận \(\overrightarrow{n_d}=\left(1;1\right)\) là 1 vtpt
Gọi \(\overrightarrow{n}=\left(a;b\right)\) là 1 vtpt của \(\Delta\), do d và \(\Delta\) tạo với nhau 1 góc 60 độ
\(\Rightarrow\dfrac{\left|a.1+b.1\right|}{\sqrt{1^2+1^2}.\sqrt{a^2+b^2}}=cos60^0=\dfrac{1}{2}\)
\(\Rightarrow\sqrt{2}\left|a+b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow2\left(a+b\right)^2=a^2+b^2\)
\(\Rightarrow a^2+4ab+b^2=0\)
Chọn \(a=1\Rightarrow\left[{}\begin{matrix}b=-2-\sqrt{3}\\b=-2+\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\) Có 2 đường thẳng \(\Delta\) thỏa mãn:
\(\left[{}\begin{matrix}1\left(x-2\right)-\left(2+\sqrt{3}\right)\left(y+6\right)=0\\1\left(x-2\right)-\left(2-\sqrt{3}\right)\left(y+6\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\left(2+\sqrt{3}\right)y-14-6\sqrt{3}=0\\x-\left(2-\sqrt{3}\right)y-14+6\sqrt{3}=0\end{matrix}\right.\)
Đường thẳng d cắt trục Ox tại A(1;0) và cắt trục Oy tại \(B\left(0;\sqrt{3}\right)\)
Ta có: \(tan\widehat{BAO}=\dfrac{OB}{OA}=\dfrac{\sqrt{3}}{1}=\sqrt{3}\Rightarrow\widehat{BAO}=30^0\)
Góc tạo bởi đường thẳng d và trục Ox là góc \(\widehat{BAx}\)
Suy ra \(\widehat{BAx}=180^0-\widehat{BAO}=180^0-30^0=150^0\)
Đs....