Cho tam giác ABC cân có góc A=90 độ.Kẻ đường thẳng d qua A.Kẻ BH;CK vuông góc d tại H;K.Chứng minh rằng:(\(BH^2+CK^2\))không phụ thuộc vào vị trí của d.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


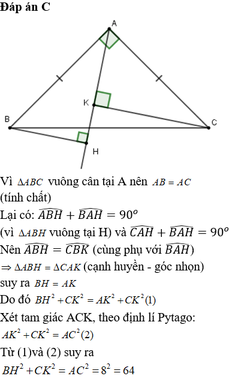
a) Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK(cạnh huyền-góc nhọn)
b) Ta có: ΔABH=ΔACK(cmt)
nên AH=AK(hai cạnh tương ứng)
Ta có: AH+HC=AC(H nằm giữa A và C)
AK+KB=AB(K nằm giữa A và B)
mà AC=AB(ΔABC cân tại A)
và AH=AK(cmt)
nên HC=KB
Ta có: ΔABH=ΔACK(cmt)
nên \(\widehat{ABH}=\widehat{ACK}\)(hai góc tương ứng)
hay \(\widehat{KBO}=\widehat{HCO}\)
Xét ΔKBO vuông tại K và ΔHCO vuông tại H có
KB=HC(cmt)
\(\widehat{KBO}=\widehat{HCO}\)(cmt)
Do đó: ΔKBO=ΔHCO(cạnh góc vuông-góc nhọn kề)
c) Ta có: IB=IC(gt)
nên I nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(2)
Ta có: OB=OC(ΔKOB=ΔHOC)
nên O nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(3)
Từ (1), (2) và (3) suy ra A,O,I thẳng hàng(đpcm)

Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [C, A] Đoạn thẳng k: Đoạn thẳng [A, M] Đoạn thẳng m: Đoạn thẳng [E, D] Đoạn thẳng n: Đoạn thẳng [E, C] Đoạn thẳng p: Đoạn thẳng [B, D] Đoạn thẳng s: Đoạn thẳng [M, I] Đoạn thẳng t: Đoạn thẳng [M, J] A = (0.26, 6.08) A = (0.26, 6.08) A = (0.26, 6.08) B = (-1.78, 1.2) B = (-1.78, 1.2) B = (-1.78, 1.2) C = (5.58, 1.02) C = (5.58, 1.02) C = (5.58, 1.02) Điểm M: Trung điểm của g Điểm M: Trung điểm của g Điểm M: Trung điểm của g Điểm E: Giao điểm của i, l Điểm E: Giao điểm của i, l Điểm E: Giao điểm của i, l Điểm D: Giao điểm của j, l Điểm D: Giao điểm của j, l Điểm D: Giao điểm của j, l Điểm K: Giao điểm của f, n Điểm K: Giao điểm của f, n Điểm K: Giao điểm của f, n Điểm H: Giao điểm của h, p Điểm H: Giao điểm của h, p Điểm H: Giao điểm của h, p Điểm I: Giao điểm của q, f Điểm I: Giao điểm của q, f Điểm I: Giao điểm của q, f Điểm J: Giao điểm của r, h Điểm J: Giao điểm của r, h Điểm J: Giao điểm của r, h
Kẻ \(MI⊥AB,MJ⊥AC\)
Ta thấy \(\widehat{EAK}=\widehat{AMI}\) (Cùng phụ với \(\widehat{KAM}\))
Vậy nên \(\Delta EAK\sim\Delta AMI\left(g-g\right)\Rightarrow\frac{EA}{AM}=\frac{AK}{MI}=2.\frac{AK}{KC}\)
Tương tự : \(\Delta DAH\sim\Delta AMJ\left(g-g\right)\Rightarrow\frac{DA}{AM}=\frac{AH}{MJ}=2.\frac{AH}{BH}\)
Mà \(\Delta AHB\sim\Delta AKC\left(g-g\right)\Rightarrow\frac{AH}{AK}=\frac{HB}{KC}\Rightarrow\frac{AH}{HB}=\frac{AK}{KC}\)
Vậy thì \(\frac{AE}{AM}=\frac{DE}{AM}\Rightarrow AE=ED.\)
Tam giác DEM có MA là đường cao đồng thời là trung tuyến nên nó là tam giác cân tại M.
Câu hỏi của Phạm Ngọc Thạch - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.