Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB, AC theo thứ tự ở D, E chia tam giác thành hai phần có diện tích bằng nhau. Tỷ số\(\frac{AD}{AB}\) bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 8 2016
Giả sử đường thẳng d song song với BC và cắt cạnh AB và AC tại D,E. Ta dễ dạng chứng minh được tam giác ADE đồng dạng tam giác ABC vì DE // BC
Khi đó : \(\frac{S_{ADE}}{S_{ABC}}=\left(\frac{AD}{AB}\right)^2=\frac{1}{2}\)
\(\Rightarrow\frac{AD}{AB}=\frac{\sqrt{2}}{2}\) (VÌ AD, AB > 0)
CM
11 tháng 12 2019
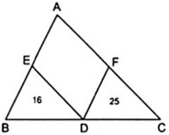
Đặt S A B C = S . Vì DE//AC nên Δ BED ∼ Δ BAC
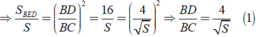
Lại có DF//AB nên Δ CDF ∼ Δ CBA
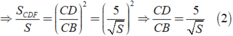
Cộng theo vế của đẳng thức ( 1 ) và ( 2 ) ta được:
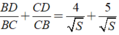
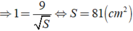
Vậy diện tích của tam giác ABC là 81 c m 2
CM
30 tháng 9 2019
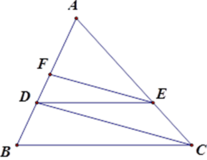
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F . A B = A D 2
Vậy 9.16 = A D 2 ó A D 2 = 144 ó AD = 12
Đáp án: C
SADE = SDEBC (gt) =>\(\frac{S_{ADE}}{S_{ABC}}=\frac{1}{2}\)
\(\Delta ADE,\Delta ABE\)có chung đường cao hạ từ E nên\(\frac{S_{ADE}}{S_{ABE}}=\frac{AD}{AB}\)
\(\Delta ABE,\Delta ABC\)có chung đường cao hạ từ B nên\(\frac{S_{ABE}}{S_{ABC}}=\frac{AE}{AC}\)
\(\Rightarrow\frac{S_{ADE}}{S_{ABE}}.\frac{S_{ABE}}{S_{ABC}}=\frac{AD}{AB}.\frac{AE}{AC}\).
\(\Delta ABC\)có DE // BC nên\(\frac{AD}{AB}=\frac{AE}{AC}\)(định lí Ta-let).Suy ra\(\frac{S_{ADE}}{S_{ABC}}=\left(\frac{AD}{AB}\right)^2\Rightarrow\frac{AD}{AB}=\frac{1}{\sqrt{2}}\)