Tìm x,y biết: 25-y2=8(x-2009)2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: =>x+y-xy=-16
=>x+y-xy-1=-17
=>x(1-y)-(1-y)=-17
=>(1-y)(x-1)=-17
=>(x-1;y-1)=17
=>(x-1;y-1) thuộc {(1;17); (17;1); (-1;-17); (-17;-1)}
=>(x,y) thuộc {(2;18); (18;2); (0;-16); (-16;0)}
b: Tham khảo:


Vì \(8\left(x-2009\right)^2\) chẵn nên \(25-y^2\) chẵn
Mà \(25\) lẻ nên \(y^2\) lẻ
Và \(25-y^2=8\left(x-2009\right)^2\ge0\Leftrightarrow y^2\le25\)
\(\Leftrightarrow y^2\in\left\{1;9;25\right\}\Leftrightarrow y\in\left\{1;3;5\right\}\left(y\in N\right)\)
\(\forall y=1\Leftrightarrow8\left(x-2009\right)^2=24\Leftrightarrow\left(x-2009\right)^2=3\left(loại\right)\\ \forall y=3\Leftrightarrow8\left(x-2009\right)^2=16\Leftrightarrow\left(x-2009\right)^2=2\left(loại\right)\\ \forall y=5\Leftrightarrow8\left(x-2009\right)^2=0\Leftrightarrow\left(x-2009\right)^2=0\Leftrightarrow x=2009\left(nhận\right)\)
Vậy \(\left(x;y\right)=\left(2009;5\right)\)
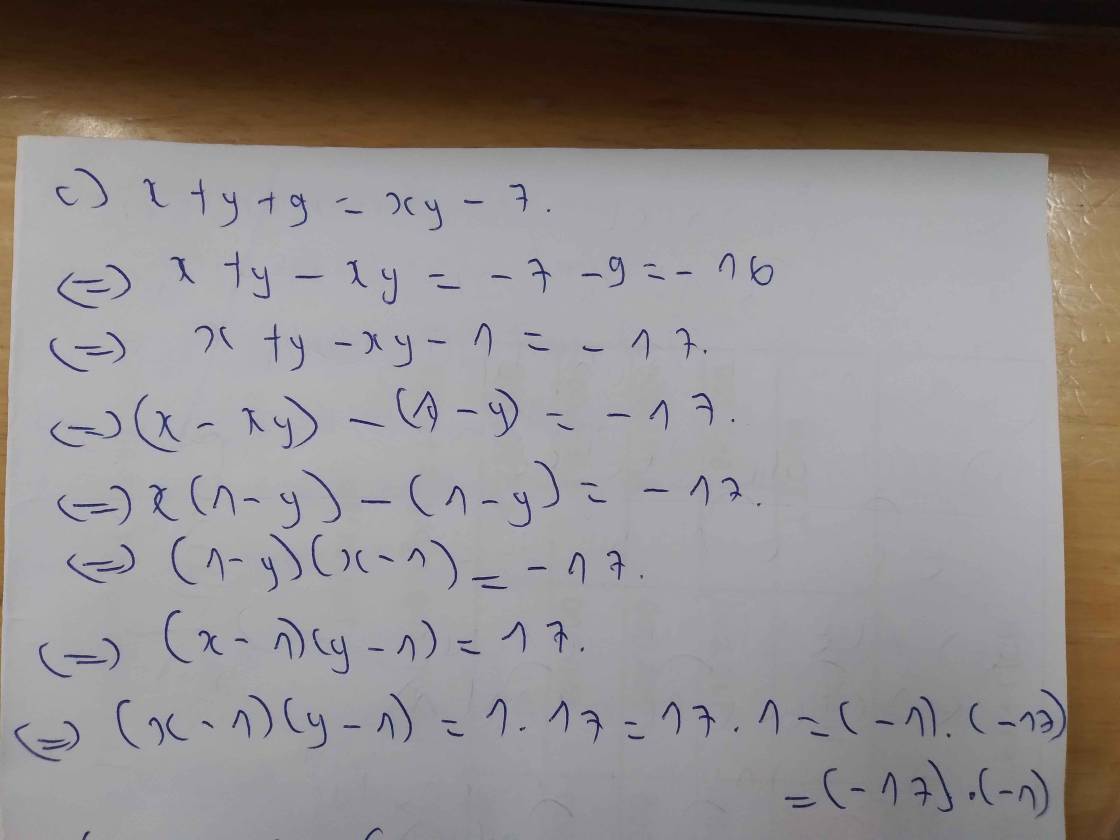

Ta có
25 - y^2 = 8(x-2009)^2
Dễ dàng thấy rằng vế phải luôn dương.Nên vế trái phải dương.Nghĩa là 25-y^2 >=0
Mặt khác do 8(x-2009)^2 chia hết cho 2.Như vậy Vế phải luôn chẳn
Do đó y^2 phải lẻ.( hiệu hai số lẽ là 1 số chẳn.hehe)
Do vậy chỉ tồn tại các giá trị sau
y^2 = 1, y^2 = 9, y^2 = 25
y^2 = 1; (x-2009)^2 = 3 (loại)
y^2 = 9; (x-2009)^2 = 2 (loại)
y^2 = 25; (x-2009)^2 = 0; x = 2009
Vậy pt có nghiệm nguyên (2009 , -5) ; (2009 , 5)
Ta có
25 - y^2 = 8(x-2009)^2
Dễ dàng thấy rằng vế phải luôn dương.Nên vế trái phải dương.Nghĩa là 25-y^2 >=0
Mặt khác do
8(x-2009)^2 chia hết cho 2.Như vậy Vế phải luôn chẳn
Do đó y^2 phải lẻ.( hiệu hai số lẽ là 1 số chẳn.hehe)
Do vậy chỉ tồn tại các giá trị sau
y^2 = 1, y^2 = 9, y^2 = 25
y^2 = 1; (x-2009)^2 = 3 (loại)
y^2 = 9; (x-2009)^2 = 2 (loại)
y^2 = 25; (x-2009)^2 = 0; x = 2009
Vậy pt có nghiệm nguyên (2009 , -5) ; (2009 , 5)