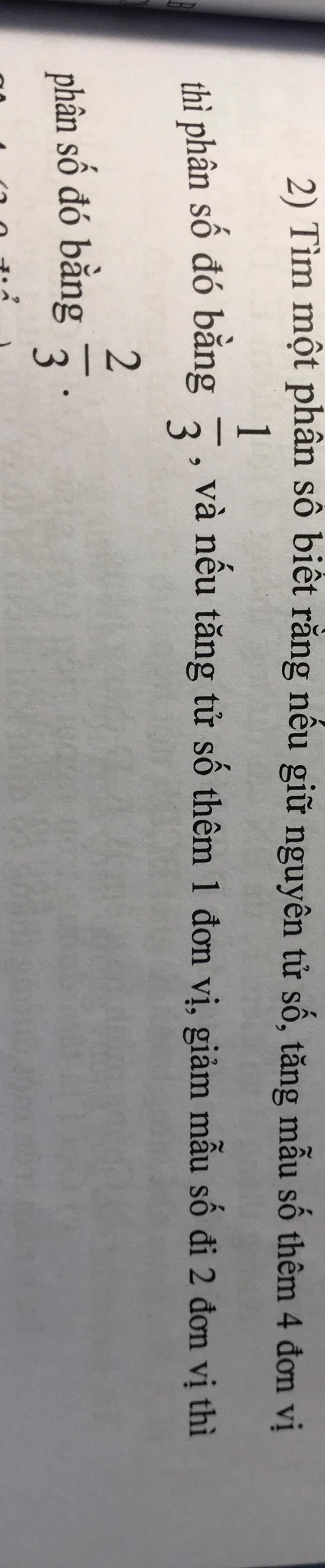Mn giải giúp em bài 4 với a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
0
H
6 tháng 9 2021
a) $n_{H_2} = 0,15(mol)$
$2Al + 6HCl \to 2AlCl_3 + 3H_2$
Theo PTHH :
$n_{Al} = \dfrac{2}{3}n_{H_2} = 0,1(mol)$
$m_{Al} = 0,1.27 = 2,7(gam)$
$m_{Cu} = 10 -2,7 = 7,3(gam)$
b)
$n_{HCl} =2 n_{H_2} = 0,3(mol)$
$C_{M_{HCl}} = \dfrac{0,3}{0,1} = 3M$
VX
0
3 tháng 10 2021
a: Xét tứ giác AMHN có
\(\widehat{MAN}=\widehat{ANH}=\widehat{AMH}=90^0\)
Do đó: AMHN là hình chữ nhật
3 tháng 10 2021
a) Xét tứ giác AMHN có:
\(\widehat{AMH}=\widehat{MAN}=\widehat{ANH}=90^0\)
=> AMHN là hình chữ nhật
b) Ta có: MH=AN(AMHN là hình chữ nhật)
AN=DN(D đối xứng với A qua N)
=> MH=DN
MH//DN(AMHN là hình chữ nhật nên MH//AN,D∈AN)
=> MHDN là hình bình hành
9 tháng 12 2023
Câu 2:
1: \(y=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)x+4=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)\cdot x=\sqrt{3}+5-4=\sqrt{3}+1\)
=>\(x=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=\dfrac{\left(\sqrt{3}+1\right)^2}{3-1}=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}\)
2: \(x^2-2\left(1-m\right)x-2m-5=0\)
=>\(x^2+\left(2m-2\right)x-2m-5=0\)
a: \(\Delta=\left(2m-2\right)^2-4\left(-2m-5\right)\)
\(=4m^2-8m+4+8m+20\)
\(=4m^2+24>=24>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Câu 1:
2: Thay x=2 và y=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2a-\left(-1\right)=5\\b\cdot2+a\cdot\left(-1\right)=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=5+\left(-1\right)=4\\2b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\2b=a+4=6\end{matrix}\right.\)
=>a=2 và b=3
2: Gọi phân số cần tìm có dạng là \(\dfrac{a}{b}\left(b\ne0\right)\)
Khi tăng mẫu số thêm 4 đơn vị thì phân số đó bằng 1/3 nên ta có:
\(\dfrac{a}{b+4}=\dfrac{1}{3}\)
=>3a=b+4
=>3a-b=4(1)
Khi giảm mẫu số đi 2 đơn vị thì phân số bằng với 2/3 nên ta có:
\(\dfrac{a}{b-2}=\dfrac{2}{3}\)
=>3a=2(b-2)
=>3a=2b-4
=>3a-2b=-4(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a-b=4\\3a-2b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\3a-b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=8\\3a=b+4=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=8\end{matrix}\right.\)(nhận)
Vậy: Phân số cần tìm là \(\dfrac{4}{8}\)
NL
3
XV
1
TP
31 tháng 7 2021
43.a) \(m_{HCl\left(bđ\right)}=200.10,95\%=21,9\left(g\right)\)
=> \(n_{HCl\left(bđ\right)}=\dfrac{21,9}{36,5}=0,6\left(mol\right)\)
b) HCl phản ứng với NaOH là HCl dư
\(HCl+NaOH\rightarrow NaCl+H_2O\)
\(n_{HCl\left(dư\right)}=n_{NaOH}=0,05.2=0,1\left(mol\right)\)
=> \(n_{HCl\left(pứ\right)}=n_{HCl\left(bđ\right)}-n_{HCl\left(dư\right)}=0,6-0,1=0,5\left(mol\right)\)
c) \(CaCO_3+2HCl\rightarrow CaCl_2+H_2O+CO_2\)
\(n_{CaCO_3}=\dfrac{1}{2}n_{HCl\left(pứ\right)}=0,25\left(mol\right)\)
=> \(m_{CaCO_3}=0,25.100=25\left(g\right)\)
d) \(n_{CO_2}=\dfrac{1}{2}n_{HCl\left(pứ\right)}=0,25\left(mol\right)\)
=> \(V_{CO_2}=0,25.22,4=5,6\left(l\right)\)
e) \(m_{ddsaupu}=25+200-0,25.44=214\left(g\right)\)
Dung dịch A gồm CaCl2 và HCl dư
\(n_{CaCl_2}=\dfrac{1}{2}n_{HCl\left(pứ\right)}=0,25\left(mol\right)\)
\(C\%_{CaCl_2}=\dfrac{0,25.111}{214}.100=12,97\%\)
\(C\%_{HCl\left(dư\right)}=\dfrac{0,1.36,5}{214}.100=1,71\%\)