Một chiếc thuyền khi xuôi dòng mất thời gian t1, khi ngược dòng mất thời gian t2. Hỏi nếu thuyền trôi theo dòng nước trên quãng đường trên sẽ mất thời gian bao lâu? ( làm ơn giải rõ ràng ra cho mình với nhé )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi quãng đường là S thì vận tốc lúc xuôi dòng và ngược dòng lần lượt là \(\frac{S}{t_1};\frac{S}{t_2}\)
vận tốc dòng nước: (v xuôi - v ngược tất cả chia 2)
\(S\left(\frac{1}{t_1}-\frac{1}{t_2}\right).\frac{1}{2}\)
thời gian tự trôi:
t=\(\frac{S}{v_n}=S.\frac{2}{S\left(\frac{1}{t_1}-\frac{1}{t_2}\right)}=\frac{2}{\frac{t_2-t_1}{t_1.t_2}}=\frac{2t_1t_2}{t_2-t_1}\)
vậy thời gian để thuyền tự trôi là \(\frac{2t_1.t_2}{t_2-t_1}\)(đvtg)

nếu thuyền trôi theo dòng nước trên quãng sống thì mất số thời gian là :
(t1 - t2) : 2

Gọi vận tốc thuyền và vận tốc dòng nước lần lượt là x ; y ( x ; y > 0 )
Theo bài ra ta có hpt \(\left\{{}\begin{matrix}\dfrac{2}{x-y}=\dfrac{4}{x+y}\\\dfrac{40}{x-y}+\dfrac{40}{x+y}=\dfrac{9}{2}\end{matrix}\right.\)
Đặt 1/(x-y) = t ; 1/(x+y) = u
\(\left\{{}\begin{matrix}2t-4u=0\\40t+40u=\dfrac{9}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}t=\dfrac{3}{40}\\u=\dfrac{3}{80}\end{matrix}\right.\)
Theo cách đặt \(\left\{{}\begin{matrix}x-y=\dfrac{40}{3}\\x+y=\dfrac{80}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=\dfrac{20}{3}\end{matrix}\right.\)(tm)
Vậy ...

Đáp án C
Gọi thuyền là (1), dòng nước là vật (2) :
![]()
Khi đi xuôi dòng v 12 → cùng phương chiều với v 2 →
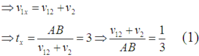
Khi đi ngược dòng v 12 → cùng phương chiều với v 2 →
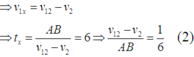
Khi thả trôi theo dòng nước thì :
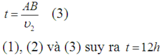
\(\Delta_t=t2-t1\)