Giải dùm bài toán sau:
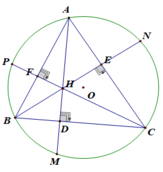
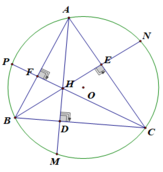
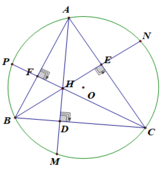
Cho tam giác nhọn ABC nội tiếp đường tròn (O) có ba đường cao AD, BE, CF đồng quy tại H. Các đường thẳng CH, BH cắt đường tròn (O) lần lượt tại các điểm thứ hai G và P. đường thẳng GD cắt (O) tại điểm K khác G.
a) Chứng minh EF//GP
b) Chứng minh đường thẳng AK đi qua trung điểm M của DE


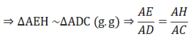
Bài toán nào em nhỉ?