Cho phân số \(\dfrac{a}{b}\)với a, b \(\inℕ^∗\). TÌm phân số x sao cho \(\dfrac{a}{b}-x=\dfrac{a}{b}\cdot x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TG
27 tháng 3 2021
\(\dfrac{a-x}{b-y}=\dfrac{a}{b}\)
\(\Rightarrow\dfrac{a-x}{a}=\dfrac{b-y}{b}\)
\(\Rightarrow1-\dfrac{x}{a}=1-\dfrac{y}{b}\)
\(\Rightarrow\dfrac{x}{a}=\dfrac{y}{b}\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{a}{b}\)
OY
1 tháng 8 2021
Bài 4:
a) \(\dfrac{2.7.13}{26.35}=\dfrac{2.7.13}{13.2.7.5}=\dfrac{1}{5}\)
b) \(\dfrac{23.5-23}{4-27}=\dfrac{23.\left(5-1\right)}{-23}=\dfrac{23.4}{-23}=-4\)
c) \(\dfrac{2130-15}{3550-25}=\dfrac{2115}{3525}=\dfrac{3}{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2021
\(y=\dfrac{4}{x}+\dfrac{9}{1-x}\ge\dfrac{\left(2+3\right)^2}{x+1-x}=25\)
Dấu "=" xảy ra khi \(\dfrac{x}{2}=\dfrac{1-x}{3}\Rightarrow x=\dfrac{2}{5}\)
\(\Rightarrow a+b=7\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 10 2021
Note: \(\sqrt{\dfrac{1}{4x}+\dfrac{\sqrt{x}+e^x}{\sqrt{x}.e^{2x}}}=\sqrt{\dfrac{1}{4x}+\dfrac{1}{e^x.\sqrt{x}}+\dfrac{1}{e^{2x}}}=\sqrt{\left(\dfrac{1}{2\sqrt{x}}+\dfrac{1}{e^x}\right)^2}=\dfrac{1}{2\sqrt{x}}+\dfrac{1}{e^x}\)
Vấn đề bây giờ có lẽ đã quá đơn giản
TC
24 tháng 4 2022
\(=>\dfrac{a}{b}\times\left(-\dfrac{2}{7}+\dfrac{5}{7}\right)=\dfrac{5}{7}\)
\(=>\dfrac{a}{b}\times\dfrac{3}{7}=\dfrac{5}{7}=>\dfrac{a}{b}=\dfrac{5}{7}:\dfrac{3}{7}=\dfrac{5}{3}\)
vậy \(\dfrac{a}{b}=\dfrac{5}{3}\)
NA
24 tháng 4 2022
\(\Rightarrow\dfrac{a}{b}\times\left(-\dfrac{2}{7}+\dfrac{5}{7}\right)=\dfrac{5}{7}\\ \Rightarrow\dfrac{a}{b}\times\dfrac{3}{7}=\dfrac{5}{7}\\ \Rightarrow\dfrac{a}{b}=\dfrac{5}{7}:\dfrac{3}{7}\\ \Rightarrow\dfrac{a}{b}=\dfrac{5}{3}\\ \Rightarrow a=5;b=3\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2021
1.
- Với \(a+b\ge4\Rightarrow A\le0\)
- Với \(a+b< 4\Rightarrow4-a-b>0\)
\(\Rightarrow A=\dfrac{a}{2}.\dfrac{a}{2}.b.\left(4-a-b\right)\)
\(\Rightarrow A\le\dfrac{1}{64}\left(\dfrac{a}{2}+\dfrac{a}{2}+b+4-a-b\right)^4=4\)
\(A_{max}=4\) khi \(\left(a;b\right)=\left(2;1\right)\)
2.
\(P=a+\dfrac{1}{2}.a.2b\left(1+2c\right)\le a+\dfrac{a}{8}\left(2b+1+2c\right)^2\)
\(P\le a+\dfrac{a}{8}\left(7-2a\right)^2=\dfrac{1}{8}\left(4a^3-28a^2+57a-36\right)+\dfrac{9}{2}\)
\(P\le\dfrac{1}{8}\left(a-4\right)\left(2a-3\right)^2+\dfrac{9}{2}\le\dfrac{9}{2}\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(\dfrac{3}{2};1;\dfrac{1}{2}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2021
Câu 3 bạn xem lại đề, mình có thể chắc chắn với bạn là đề sai
Ví dụ bạn cho \(x=98,y=100\) thì vế trái chỉ lớn hơn 8 một chút
Đề đúng phải là: \(\left(x+y\right)\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+\dfrac{16xy}{\left(x-y\right)^2}\ge12\)
13 tháng 7 2023
Theo đề, ta có hệ:
b-a=21 và a/b=16/23
=>a-b=-21 và 23a-16b=0
=>a=48 và b=69
Phân số cần tìm là 48/69
11 tháng 12 2023
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{3x+1}-2}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{3x+1-4}{\sqrt{3x+1}+2}\cdot\dfrac{1}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{3x-3}{\left(x-1\right)\left(x+1\right)\left(\sqrt{3x+1}+2\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{3}{\left(x+1\right)\left(\sqrt{3x+1}+2\right)}=\dfrac{3}{\left(1+1\right)\left(\sqrt{3+1}+2\right)}\)
\(=\dfrac{3}{2\cdot4}=\dfrac{3}{8}\)
=>a=3;b=8
=>a2+b=9+8=17
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2021
\(\dfrac{\pi}{2}< a< \pi\Rightarrow sina>0\)
\(\Rightarrow sina=\sqrt{1-cos^2a}=\dfrac{\sqrt{5}}{3}\)
\(K=2sina.cosa+2cos^2a-1=-\dfrac{1}{9}-\dfrac{4}{9}\sqrt{5}\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{1}{4}\Rightarrow a-b=-3\)
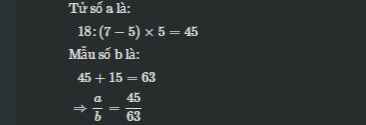
Ta có:
\(\dfrac{a}{b}-x=\dfrac{a}{b}x\\ \Leftrightarrow\dfrac{a}{b}x+x=\dfrac{a}{b}\\ \Leftrightarrow x\left(\dfrac{a}{b}+1\right)=\dfrac{a}{b}\\ \Leftrightarrow x\left(\dfrac{a+b}{b}\right)=\dfrac{a}{b}\\ \Rightarrow x=\dfrac{a}{b}:\dfrac{a+b}{b}=\dfrac{a}{b}.\dfrac{b}{a+b}=\dfrac{a}{a+b}\\ \)
Đs...