Một ô tô đang chạy với vận tốc 22 m/s lên dốc, chuyển động chậm dần đều với gia tốc 0,4 m/s2. Cùng lúc đó, một xe đạp đang đi với vận tốc 2 m/s thì xuống dốc chuyển động nhanh dần đều với gia tốc 0,2 m/s2. Biết dốc dài 840 m. Vị trí hai xe gặp nhau trên dốc cách chân dốc là

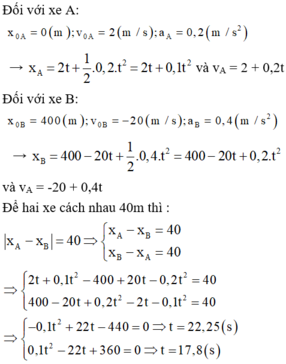
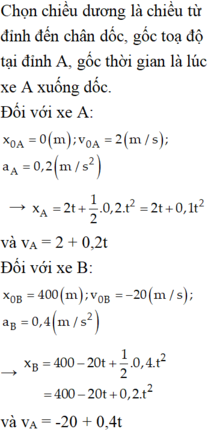

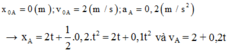
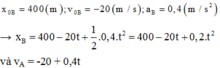

Quãng đường ô tô đi đến lúc gặp xe đạp là:
\(x_1=\dfrac{1}{2}at^2+v_0t=\dfrac{1}{2}\left(-0,4\right)t^2+22t=-0,2t^2+22t\)
Quãng đường xe đạp đi được đến lúc gặp xe ô tô là:
\(x_2=\dfrac{1}{2}a_2t^2+v_2t=\dfrac{1}{2}.0,2t^2+2t=0,1t^2+2t\)
Lại có: \(x_1+x_2=840\Leftrightarrow-0,2t^2+22t=0,1t^2+2t\)
\(\Rightarrow t=\dfrac{200}{3}\left(s\right)\)
Vị trí hai xe gặp nhau trên dốc cách chân dốc là: \(x_1=-0,2.\left(\dfrac{200}{3}\right)^2+\dfrac{22.200}{3}=577,78\left(m\right)\)