cho mình hỏi đồ thị hàm số cắt nhau khi a=a', b#b' đúng không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 6 2017
Đáp án C.
Phương trình hoành độ giao điểm của hai đồ thị là x 2 - x = 5 + 3 : x ⇔ x - 3 x + 1 2 = 0 ⇔ x ∈ 3 ; - 1 ⇒ A 3 ; 6 , B - 1 ; 2 ⇒ B A → 4 ; 4 ⇒ A B = 4 2 .
CM
26 tháng 12 2017
Đáp án C
Hàm số y = log a x nhận Oy làm tiệm cận đứng , đồng biến nếu a>1, nghịch biến nếu 0<a<1
Hàm số y = a x nhận Ox làm tiệm cận ngang, đồng biến nếu a>1, nghịch biến nếu 0<a<1
Đồ thị hàm số y = log a x và đồ thị hàm số y = a x cắt nhau tại 2 điểm phân biệt hoặc không cắt nhau nếu a>1
Vậy mệnh đề I, IV sai
Mệnh đề II, III đúng
26 tháng 1
a: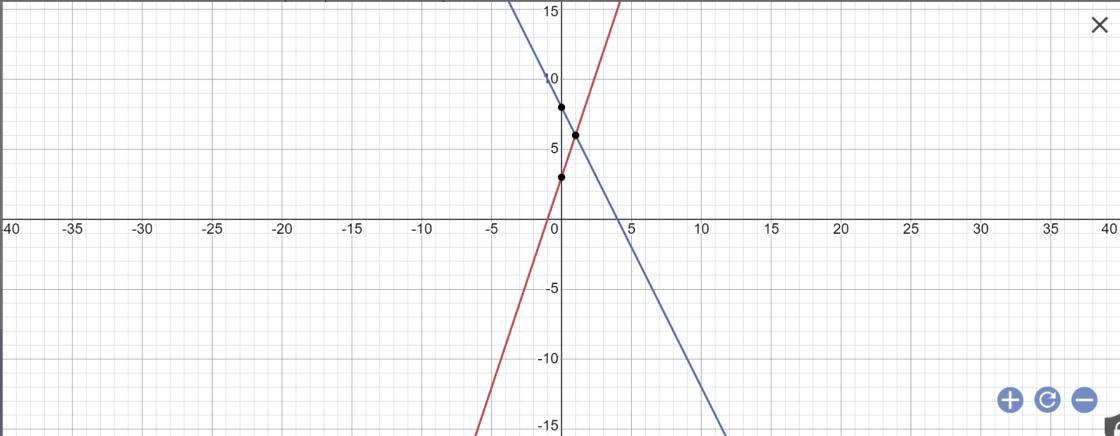 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}3x+3=-2x+8\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=-2+8=6\end{matrix}\right.\)
Vậy: A(1;6)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\3x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-2x+8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-2x=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
Vậy: A(1;6); B(-1;0); C(4;0)
\(AB=\sqrt{\left(-1-1\right)^2+\left(0-6\right)^2}=2\sqrt{10}\)
\(AC=\sqrt{\left(4-1\right)^2+\left(0-6\right)^2}=3\sqrt{5}\)
\(BC=\sqrt{\left(4+1\right)^2+\left(0-0\right)^2}=5\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot BA\cdot AC}=\dfrac{40+45-25}{2\cdot2\sqrt{10}\cdot3\sqrt{5}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot2\sqrt{10}\cdot3\sqrt{5}=15\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
Tọa độ giao điểm của \(y=-2x+k\) và trục hoành: \(y=0\Rightarrow x=\dfrac{k}{2}\)
Tọa độ giao điểm \(y=-2x+k\) với trục tung: \(x=0\Rightarrow y=k\)
Tọa độ giao điểm của \(y=3x-k+4\) với trục hoành: \(y=0\Rightarrow x=\dfrac{k-4}{3}\)
Tọa độ giao điểm của \(y=3x-k+4\) với trục tung: \(x=0\Rightarrow y=-k+4\)
a. Đồ thị các hàm cắt nhau tại 1 điểm trên trục tung khi:
\(k=-k+4\Rightarrow x=2\)
b. Đồ thị các hàm cắt nhau tại 1 điểm trên trục hoành khi:
\(\dfrac{k}{2}=\dfrac{k-4}{3}\Rightarrow k=-8\)
VH
16 tháng 11 2021
vẽ đồ thị hàm số y=/x/+4x . Với giá trị nào của k thì hàm số y=k cắt đồ thị hàm số trên tại hai điểm phân biệt
5 tháng 8 2019
Khi x = 1 => y = -2
Khi x = 2 => y = -4
Vẽ đồ thị hàm số A(1 ; -2 ) và A( 2 ; -2 )
b) thay x = -1 vào hàm số y = -2x ta được
y = -2 . ( -1 ) = 2
=> A( - 1; 2 ) là điểm có thuộc đồ thị hàm số đã cho
5 tháng 8 2019
Em đăng nhầm đề bài câu c rồi nhé.
Khi biết hoành độ của B là 3
c) Gọi tọa độ điểm B là: B(x; y) với x=3
Theo bài ra B thuộc đồ thị hàm số
=> y=-2x=-2.3=-6
=> Tung đôh của điểm B là -6
9 tháng 8 2021
a, bạn tự vẽ nhé
b, Để hàm số nghịch biến khi m < 0
c, đths y = mx + 2m - 1 cắt trục tung tại điểm có tung độ bằng 3
Thay x = 0 ; y = 3 ta được : \(2m-1=3\Leftrightarrow m=2\)
d, đths y = mx + 2m - 1 cắt trục hoành tại điểm có hoành độ bằng -3
Thay x = -3 ; y = 0 ta được : \(-3m+2m-1=0\Leftrightarrow-m-1=0\Leftrightarrow m=-1\)
9 tháng 8 2021
bổ sung hộ mình nhé
( dòng đầu tiên ) Để đths trên là hàm bậc nhất khi \(m\ne0\)
5 tháng 12 2021
a, Thay x = -2 => y = -2 + 4 = 2 => A(-2;2)
(d) cắt y = x + 4 tại A(-2;2) <=> 2 = -2 ( m + 1 ) - 2
<=> -2m - 2 - 2 = 2 <=> -2m = 6 <=> m = -3
Vậy (d) : y = -2x - 2
b, bạn tự vẽ nhé
c, Cho x = 0 => y = -2
=> (d) cắt trục Oy tại A(0;-2) => OA = | -2 | = 2
Cho y = 0 => x = -1
=> (d) cắt trục Ox tại B(-1;0) => OB = | -1 | = 1
Ta có : \(S_{OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}.2.1=1\)( dvdt )
5 tháng 12 2021
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\hept{m+5=22m−10≠−1\hept{m+5=22m−10≠−1 <=> \hept{m=−3m≠92\hept{m=−3m≠92 <=> m=−3
Giả sử (d) luôn đi qua điểm cố định M(x0; y0)
Ta có: y0=(m+5)x0+2m−10y0=(m+5)x0+2m−10
<=> mx0+5x0+2m−10−y0=0mx0+5x0+2m−10−y0=0
<=> m(xo+2)+5x0−y0−10=0m(xo+2)+5x0−y0−10=0
Để M cố định thì: \hept{x0+2=05x0−y0−10=0\hept{x0+2=05x0−y0−10=0 <=> \hept{x0=−2y0=−20\hept{x0=−2y0=−20
Vậy...