Tìm a,b để 3a4b5 chia hết cho 9 và a-b=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
4
NK
1
5 tháng 8 2020
Bài làm:
Vì a,b, là các chữ số
=> a,b không âm
Mà a + b = -10
=> Sẽ phải tồn tại ít nhất 1 trong 2 số a,b âm
Mâu thuẫn với điều kiện nêu trên
=> không tồn tại a,b thỏa mãn yêu cầu đề bài
PP
8
25 tháng 3 2017
các số tự nhiên a và 6a có tổng các chữ số như nhau. chứng minh rằng a chia hết cho 9
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 9 2023
c, \(\overline{b852a}\) ⋮ 3; 4
\(\overline{b852a}\) ⋮ 4 ⇒ a = 4; 0
a = 4; \(\overline{b852a}\) ⋮ 3 ⇒ b + 8 + 5 + 2 + a ⋮ 3 ⇒ b + 15 + 4 ⋮ 3
⇒ b + 1 ⋮ 3 ⇒ b = 2; 5; 8
⇒ \(\overline{b852a}\) = 28524; 58524; 88524;
a = 0; \(\overline{b852a}\) ⋮ 3 ⇒ b + 8 + 5 + 2 + a ⋮ 3 ⇒ b + 15+ 0 ⋮ 3
⇒ b ⋮ 3 ⇒ b = 3; 6;9
⇒ \(\overline{b852a}\) = 38520; 68520; 98520
Vậy \(\overline{b852a}\) = 28524; 38520; 58524; 68520; 88524; 98520
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 9 2023
d, \(\overline{35a7b}\) \(⋮\) 4 ; 9
\(\overline{35a7b}\) ⋮ 4 ⇒ b = 2; 6
b = 2; \(\overline{35a7b}\) ⋮ 9 ⇒ 3+5+a+7+b ⋮ 9 ⇒ a + 15+2 ⋮ 9 ⇒ a - 1 ⋮ 9
⇒ a = 1
⇒ \(\overline{35a7b}\) = 35172
b = 6; \(\overline{35a7b}\) ⋮ 9 ⇒ 3 + 5 + a + 7 + 6 ⋮ 9 ⇒ a + 3 ⋮ 9
⇒ a = 6
⇒ \(\overline{35a7b}\) = 35676
⇒ \(\overline{35ab7}\) = 35172; 35676
NT
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
6 tháng 8 2015
3a4b5=30405+1000xa+10xb=(30404+1001xa+11xb)-(a+b-1)
Ta thấy (30404+1001xa+11xb) chia hết cho 11 => a+b-1 phải chia hết cho 11
=> a+b=12
=> b=(12-2):2=5 => a=b+2=5+2=7
17 tháng 8 2015
3a4b5 chia hết cho 9
=> 12 + a + b chia hết cho 9
=> a + b = 6 hoặc a + b = 15
Mà nếu a+ b = 15
=> a = (15 + 2) : 2 nên loại
Vậy a+b =6
=> a = (6+2) : 2 = 4
=> b = 6 - 4 = 2
Vậy số cần tìm là 34425
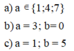
3a4b5 : hết 9 ; a-b = 5 => a = 6 ; b = 1