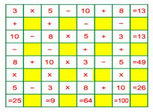
điền vào ô trống trên các số từ:0;1;2;3;........;8;9;10.Để các hàng ngang,dọc,chéo đều có tổng là 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
điền vào ô trống trên các số từ:0;1;2;3;........;8;9;10.Để các hàng ngang,dọc,chéo đều có tổng là 10


Ta có:
687+405=1092
1092×135=147420
147420−16852=130568
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là 1092; 147420; 130568.

Ta có:
0 , 75 × 10 = 7 , 5 ; 18 , 47 × 100 = 1847 ; 0 , 732 × 10000 = 7320
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái qua phải là 7,5; 1847; 7320.


Ta có thể xét các tổng theo từng hàng, từng cột và không khó khăn lắm sẽ có kết quả sau:

Chữ số 6 trong số 609287 nằm ở hàng trăm nghìn nên có giá trị là 600000.
Chữ số 6 trong số 143682 nằm ở hàng chục nên có giá trị là 600.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là 600000;600.
TL:
giả sử ta tìm được cách sắp sếp các số trên như sau:
abc
def
nml
gọi giá trị số trong các ô lần lượt là a, b, c, d, e, f, m, l, n (với các số tự nhiên có giá trị từ 0 đến 10).
Ta được 8 phương trình như sau:
a + b + c = 10 (1)
d + e + f = 10 (2)
m + n + l = 10 (3)
a + d + m = 10 (4)
b + e + n = 10 (5)
c + f + l = 10 (6)
a + e + l = 10 (7)
c + e + m = 10 (8)
Từ phương trình (2), (5), (7), (8) suy ra: d + f = b + n = a + l = c + m
Lấy phương trình (1) cộng phương trình (3) ta được:
20 = a + b + c + m + n + l = (a + l) + (b + n) + (c + m) = 3 x (b + n)
=> b + n = 20/3
Thay vào phương trình (5) ta được: e = 10/3
Như vậy, trong mọi trường hợp thì số chính giữa hình vuông luôn bằng 10/3 nên đáp án bài toán là vô nghiệm.
=> Không tìm được cách sắp xếp các số 0,1,2,..10 như yêu cầu.
Gọi giá trị số trong các ô lần lượt là a, b, c, d, e, f, m, l, n (với các số tự nhiên có giá trị từ 0 đến 10).
Ta được 8 phương trình như sau:
a + b + c = 10 (1)
d + e + f = 10 (2)
m + n + l = 10 (3)
a + d + m = 10 (4)
b + e + n = 10 (5)
c + f + l = 10 (6)
a + e + l = 10 (7)
c + e + m = 10 (8)
Từ phương trình (2), (5), (7), (8) suy ra: d + f = b + n = a + l = c + m
Lấy phương trình (1) cộng phương trình (3) ta được:
20 = a + b + c + m + n + l = (a + l) + (b + n) + (c + m) = 3 x (b + n)
=> b + n = 20/3
Thay vào phương trình (5) ta được: e = 10/3
Như vậy, trong mọi trường hợp thì số chính giữa hình vuông luôn bằng 10/3 nên đáp án bài toán này là vô nghiệm.