Gọi m,n lần lượt là trung điểm của ab; cd . Chứng minh Sabcd < 1/2 . (am+an)2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔCAB có
N là trung điểm của AB
NP//AB
=>P là trung điểm của AC
Xét ΔCAB có
N là trung điểm của BC
NM//AC
=>M là trung điểm của AB
b: Xét tứ giác ANCE có
P là trung điểm chung của AC và NE
AC vuông góc NE
=>ANCE là hình thoi

* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
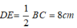
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D

Câu 2:
Theo đề bài, ta có:
AC+ CB= AB= 6(cm)
AM= MC= 1/2 AM
CN= NB= 1/2 BC
=> MC+NC= 1/2 AB
Mà: MC+ NC= MN
=> MN= 1/2 AB= 1/2 . 6= 3( cm)
Sao MC = 1/2 AC; CN = 1/2 BC mà MC + NC = 1/2 AB, phải là bằng AB chứ

a: Ta có: I và D đối xứng nhau qua AB
nên AB là đường trung trực của DI
Suy ra: AD=AI
hay AB là tia phân giác của \(\widehat{IAD}\)
Ta có: I và E đối xứng nhau qua AC
nên AC là đường trung trực của IE
Suy ra: AI=AE
hay AC là tia phân giác của \(\widehat{EAI}\)
Ta có: \(\widehat{EAD}=\widehat{EAI}+\widehat{DAI}\)
\(=2\left(\widehat{BAI}+\widehat{CAI}\right)\)
\(=2\cdot90^0=180^0\)
Suy ra:E,A,D thẳng hàng
mà AD=AE(=AI)
nên A là trung điểm của DE

a: Xét hình thang BDEC có
M là trung điểm của BD
N là trung điểm của EC
Do đó: MN là đường trung bình của hình thang BDEC
Suy ra: \(MN=\dfrac{DE+BC}{2}=\dfrac{8+4}{2}=6\left(cm\right)\)

a: Xét ΔBAC có E,F lần lượt là trung điểm của BA,BC
=>EF là đường trung bình
=>EF//AC và EF=AC/2
Xét ΔDAC có
H,G lần lượt là trung điểm của DA,DC
=>HG là đường trung bình
=>HG//AC và HG=AC/2
=>EF//HG và EF=HG
Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình
=>EH=BD/2
=>EH=AC/2=EF
Xét tứ giác EHGF có
EF//GH
EF=GH
EH=EF
Do đó: EHGF là hình thoi
b: Xét ΔEHF có Q,M lần lượt là trung điểm của EH,EF
=>QM là đường trung bình
=>QM//HF và QM=HF/2
Xét ΔGHF có
P,N lần lượt là trung điểm của GH,GF
=>PN là đường trung bình
=>PN//HF và PN=HF/2
=>QM//PN và QM=PN
Xét ΔHEG có HQ/HE=HP/HQ=1/2
nên PQ//EG
=>PQ vuông góc HF
=>PQ vuông góc QM
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc PQM=90 độ
Do đó: MNPQ là hình chữ nhật

a: Xét tứ giác AHBD có
M là trung điểm chung của AB và HD
góc AHB=90 độ
=>AHBD là hình chữ nhật
Xét tứ giác AHCE có
N là trung điểm chung của AC và HE
góc AHC=90 độ
=>AHCE là hình chữ nhật
AE//CH
=>AE//BH
mà AD//BH
nên A,D,E thẳng hàng
mà DA=AE
nên A là trung điểm của DE
Xét tứ giác BDEC có
DE//BC
DE=BC
góc DBC=90 độ
=>BDEC là hình chữ nhật
b: Xét tứ giác ABHE có
AE//HB
AE=HB
=>ABHE là hình bình hành
=>AH cắt BE tại trung điểm của mỗi đường(1)
Xét tứ giác ADHC có
AD//HC
AD=HC
=>ADHC là hbh
=>AH cắt CD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra BE cắt CD tại trung điểm của AH
c: Xét ΔHDE có
HA vừa là đường cao, vừa là trung tuyến
=>ΔHDE cân tại H
=>HD=HE
BDEC là hcn
=>BE=CD