cho tam giác ABC có góc BAC = 40, trên cạnh AB,AC lần lượt lấy các điểm D và E sao cho BD = EC. Gọi M là trung điểm của DE, trên tia đối của tia MB lấy P sao cho MB = MP. Tính góc PCE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 2 2020
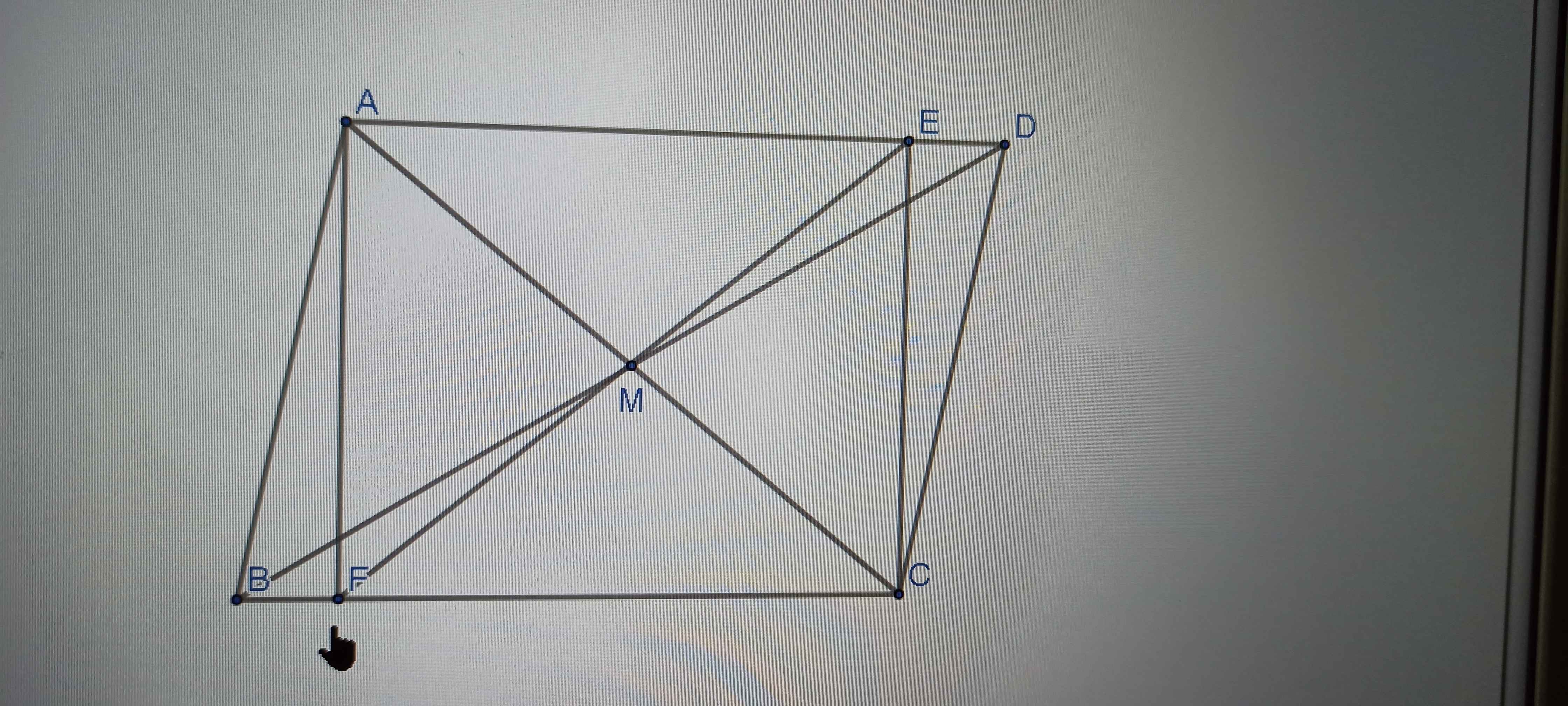
Bài làm
a) Xét tam giác MDB và tam giác MEF có:
DM = ME ( M là trung điểm DE )
\(\widehat{DMB}=\widehat{EMC}\) ( hai góc đối )
BM = MF ( gt )
=> Tam giác MDB = tam giác MEF ( c.g.c )
b) Vì tam giác MDB = tam giác MEF ( cmt )
=> EF = BD ( hai cạnh tương ứng )
Mà BD = EC ( gt )
=> EF = EC
=> Tam giác CEF cân tại E ( đpcm )
c)
CH
Cô Hoàng Huyền
Admin
VIP
2 tháng 2 2018
a) Xét tam giác MBD và tam giác MFE có:
MB = MF (gt)
MD = ME (gt)
\(\widehat{DMB}=\widehat{EMF}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta MBD=\Delta MFE\left(c-g-c\right)\)
b) Do \(\Delta MBD=\Delta MFE\Rightarrow BD=FE\)
Mà BD = EC nên EF = EC.
Vậy tam giác CEF cân tại E.
c) Do \(\Delta MBD=\Delta MFE\Rightarrow\widehat{BDM}=\widehat{FEM}\)
Mà chúng lại ở vị trí so le trong nên AB // FE.
Suy ra \(\widehat{BAC}=\widehat{AEF}\)
Lại có \(\widehat{BAC}=2\widehat{KAE}\) (Tính chất phân giác)
\(\widehat{AEF}=2\widehat{FCE}\) (Góc ngoài tại đỉnh cân)
\(\Rightarrow\widehat{KAE}=\widehat{ECF}\)
Chúng lại ở vị trí so le trong nên AK // CF.
16 tháng 7 2021
Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.
LL
13 tháng 1 2022
vào đây tham khảo nhé
https://olm.vn/hoi-dap/detail/98773432332.html
13 tháng 1 2022
a: Xét ΔMDB và ΔMEF có
MD=ME
\(\widehat{DMB}=\widehat{EMF}\)
MB=MF
Do đó: ΔMDB=ΔMEF
b: Ta có: ΔMDB=ΔMEF
nên EF=DB=EC
hay ΔECF cân tại E
12 tháng 3 2017
câu d vẽ tam giác đều ACO .từ o kẻ đường vuông góc với hk tại p.tam giác CAH BẰNG tam giác COP cạnh huyền góc nhọn. suy ra CP=AH SUY RA PK=PC=AH.tam giác OKP BẰNG tam giác OCP C.G.C SUY RA GÓC OKC = 15 . GÓC AKC=30 suy ra góc KAC = 180-30-75=75 SUY RA BAK=45
Nhãn
DK
6 tháng 2 2021
a) Xét ΔABF và ΔCNF có:
AF = CF (F là trung điểm của AC)
∠AFB = CFN (2 góc đối đỉnh)
FB = FN (gt)
⇒ ΔABF = ΔCNF (c.g.c)
⇒ ∠ABF = ∠CNF (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong ⇒ AB // NC
Xét ΔACE và ΔBME có:
AE = BE (E là trung điểm của AB)
∠AEC = ∠BEM (2 góc đối đỉnh)
EC = EM (gt)
⇒ ΔACE = ΔBME (c.g.c)
⇒ ∠ACE = ∠BME (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong ⇒ AC // MB
b) Xét ΔANF và ΔCBF có:
AF = CF (F là trung điểm của AC)
∠AFN = ∠CFB (2 góc đối đỉnh)
FN = FB (gt)
⇒ ΔANF = ΔCBF (c.g.c)
⇒ ∠ANF = ∠CBF (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong ⇒ AN // BC (1)
Xét ΔAME và ΔBCE có:
AE = BE (E là trung điểm của AB)
∠AEM = ∠BEC (2 góc đối đỉnh)
EM = EC (gt)
⇒ ΔAME = ΔBCE (c.g.c)
⇒ ∠AME = ∠BCE (2 góc tương ứng)
mà 2 góc ở vị trí so le trong ⇒ AM // BC (2)
Từ (1) và (2) ⇒ 3 điểm M, A, N thẳng hàng
c) Ta có: ΔANF = ΔCBF (theo b)
⇒ AN = BC (2 cạnh tương ứng) (3)
Ta có: ΔAME = ΔBCE (theo b)
⇒ AM = BC (2 cạnh tương ứng) (4)
Từ (3) và (4) ⇒ AM = AN
chào bạn!! :v