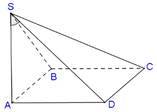
cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt đáy. Góc giữa SD và mp (SAB) bằng 600 . Tính thể tích của khối S.ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Ta có
A D ⊥ A B A D ⊥ S A ⇔ A D ⊥ S A B .
Vậy S D , S A B = S D , S A = A S D ^ = 60 0 .
Trong tam giác vuông SAD ta có
Vậy thể tích khối chóp S.ABCD bằng S A = A D . cot A S D ^ = 2 a 3 . V S A B C D = 1 3 S A B C D . S A = 1 3 4 a 2 . 2 a 3 = 8 3 a 3 9 .

Đáp án B

Ta có: S B A ^ = 60 ∘ ⇒ S A = A B tan 60 ∘ = a 3
V A . A C D = 1 3 S A . S A C D = 1 3 . a 3 . a 2 2 = a 3 3 6
Lại có: V S . A M N V S . A C D = S M S C . S N S D = 1 4 ⇒ V S . A M N = a 3 3 24
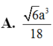
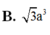
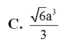
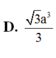

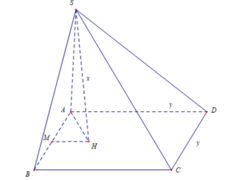

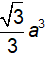
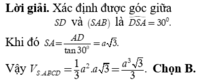
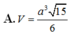
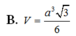
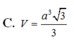
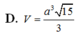


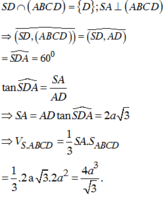
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow\widehat{DSA}\) là góc giữa SD và (SAB)
\(\Rightarrow\widehat{DSA}=60^0\)
\(\Rightarrow SA=\dfrac{AD}{tan60^0}=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow V_{S.ABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{a^3\sqrt{3}}{18}\)
{SA⊥(ABCD)⇒SA⊥ADAD⊥AB \Rightarrow AD\perp\left(SAB\right)⇒AD⊥(SAB)
\Rightarrow\widehat{DSA}⇒DSA là góc giữa SD và (SAB)
\Rightarrow\widehat{DSA}=60^0⇒DSA=600
\Rightarrow SA=\dfrac{AD}{tan60^0}=\dfrac{a\sqrt{3}}{3}⇒SA=tan600AD=3a3
\Rightarrow V_{S.ABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{a^3\sqrt{3}}{18}⇒VS.ABC=31SA.21AB.AC=18a33