Giải phương trình nghiệm nguyên
a)\(3^x-y^3=1\)
b)\(1+x+x^2+x^3=2^y\)
c)\(x^4+\left(x+1\right)^4=y^2+\left(y+1\right)^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 10 2021
\(1,\\ b,\Leftrightarrow\left(x^2+4x+4\right)+\left(y-1\right)^2=25\\ \Leftrightarrow\left(x+2\right)^2+\left(y-1\right)^2=25\)
Vậy pt vô nghiệm do 25 ko phải tổng 2 số chính phương
\(2,\\ a,\Leftrightarrow x^2-\left(y^2-6y+9\right)=47\\ \Leftrightarrow x^2-\left(y-3\right)^2=47\)
Mà 47 ko phải hiệu 2 số chính phương nên pt vô nghiệm
\(b,\Leftrightarrow\left(x-2\right)^2+\left(3y-1\right)^2=16\)
Mà 16 ko phải tổng 2 số chính phương nên pt vô nghiệm
5 tháng 10 2021
2b,
Vì 16 ko đồng dư với 1 (mod 4) nên 16 ko phải là tổng 2 scp
Định lý Fermat về tổng của hai số chính phương – Wikipedia tiếng Việt
vô đây đọc nhé
12 tháng 11 2023
a:
ĐKXĐ: \(x\notin\left\{\dfrac{3}{2};1\right\}\)
\(y=\dfrac{\left(x-2\right)^2}{\left(2x-3\right)\left(x-1\right)}=\dfrac{x^2-4x+4}{2x^2-2x-3x+3}\)
=>\(y=\dfrac{x^2-4x+4}{2x^2-5x+3}\)
=>\(y'=\dfrac{\left(x^2-4x+4\right)'\left(2x^2-5x+3\right)-\left(x^2-4x+4\right)\left(2x^2-5x+3\right)'}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{\left(2x-4\right)\left(2x^2-5x+3\right)-\left(2x-5\right)\left(x^2-4x+4\right)}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{4x^3-10x^2+6x-8x^2+20x-12-2x^3+8x^2-8x+5x^2-20x+20}{\left(2x^2-5x+3\right)^2}\)
=>\(y'=\dfrac{2x^3-5x^2-2x+8}{\left(2x^2-5x+3\right)^2}\)
b:
ĐKXĐ: x<>-3
\(y=\left(x+3\right)+\dfrac{4}{x+3}\)
=>\(y'=\left(x+3+\dfrac{4}{x+3}\right)'=1+\left(\dfrac{4}{x+3}\right)'\)
\(=1+\dfrac{4'\left(x+3\right)-4\left(x+3\right)'}{\left(x+3\right)^2}\)
=>\(y'=1+\dfrac{-4}{\left(x+3\right)^2}=\dfrac{\left(x+3\right)^2-4}{\left(x+3\right)^2}\)
y'=0
=>\(\left(x+3\right)^2-4=0\)
=>\(\left(x+3+2\right)\left(x+3-2\right)=0\)
=>(x+5)(x+1)=0
=>x=-5 hoặc x=-1
c:
ĐKXĐ: x<>-2
\(y=\dfrac{\left(5x-1\right)\left(x+1\right)}{x+2}\)
=>\(y=\dfrac{5x^2+5x-x-1}{x+2}=\dfrac{5x^2+4x-1}{x+2}\)
=>\(y'=\dfrac{\left(5x^2+4x-1\right)'\left(x+2\right)-\left(5x^2+4x-1\right)\left(x+2\right)'}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{\left(5x+4\right)\left(x+2\right)-\left(5x^2+4x-1\right)}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{5x^2+10x+4x+8-5x^2-4x+1}{\left(x+2\right)^2}\)
=>\(y'=\dfrac{10x+9}{\left(x+2\right)^2}\)
\(y'\left(-1\right)=\dfrac{10\cdot\left(-1\right)+9}{\left(-1+2\right)^2}=\dfrac{-1}{1}=-1\)
d:
ĐKXĐ: x<>2
\(y=x-2+\dfrac{9}{x-2}\)
=>\(y'=\left(x-2+\dfrac{9}{x-2}\right)'=1+\left(\dfrac{9}{x-2}\right)'\)
\(=1+\dfrac{9'\left(x-2\right)-9\left(x-2\right)'}{\left(x-2\right)^2}\)
=>\(y'=1+\dfrac{-9}{\left(x-2\right)^2}=\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}\)
y'=0
=>\(\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}=0\)
=>\(\left(x-2\right)^2-9=0\)
=>(x-2-3)(x-2+3)=0
=>(x-5)(x+1)=0
=>x=5 hoặc x=-1
24 tháng 1 2021
a) Ta có: \(\left\{{}\begin{matrix}2\left(x+1\right)-3\left(y-2\right)=5\\-4\left(x-2\right)+5\left(y-3\right)=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2-3y+6=5\\-4x+8+5y-15=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-3\\-4x+5y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-6y=-6\\-4x+5y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-y=0\\2x-3y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x-3\cdot0=-3\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=0\end{matrix}\right.\)
Vậy: hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=0\end{matrix}\right.\)
b) Ta có: \(\left\{{}\begin{matrix}8\left(x-3\right)-3\left(y+1\right)=-2\\3\left(x+2\right)-2\left(1-y\right)=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8x-24-3y-3=-2\\3x+6-2+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8x-3y=25\\3x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y=75\\24x+16y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-25y=67\\3x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-67}{25}\\3x=1-2y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=1-2\cdot\dfrac{-67}{25}=\dfrac{159}{25}\\y=-\dfrac{67}{25}\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x=\dfrac{53}{25}\\y=-\dfrac{67}{25}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{53}{25}\\y=-\dfrac{67}{25}\end{matrix}\right.\)
24 tháng 1 2021
a) HPT \(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-3\\-4x+5y=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x-6y=-6\\-4x+5y=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-y=0\\x=\dfrac{3y-3}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm \(\left(x;y\right)=\left(-\dfrac{3}{2};0\right)\)
b) HPT \(\Leftrightarrow\left\{{}\begin{matrix}8x-3y=25\\3x+2y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}16x-6y=50\\9x+6y=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}25x=53\\y=\dfrac{1-3x}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{53}{25}\\y=-\dfrac{67}{25}\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm \(\left(x;y\right)=\left(\dfrac{53}{25};-\dfrac{67}{25}\right)\)
5 tháng 10 2021
a, TK: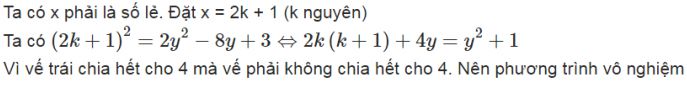
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương
6 tháng 4 2021
Bài 2:
a) Ta có: \(\Delta=\left(m-1\right)^2-4\cdot1\cdot\left(-m^2-2\right)\)
\(=m^2-2m+1+4m^2+8\)
\(=5m^2-2m+9>0\forall m\)
Do đó, phương trình luôn có hai nghiệm phân biệt với mọi m
H
6 tháng 4 2021
Bài 1:
ĐKXĐ \(2x\ne y\)
Đặt \(\dfrac{1}{2x-y}=a;x+3y=b\)
HPT trở thành
\(\left\{{}\begin{matrix}a+b=\dfrac{3}{2}\\4a-5b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}-b\\4\left(\dfrac{3}{2}-b\right)-5b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}-b\\6-9b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{8}{9}\\a=\dfrac{11}{18}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\dfrac{8}{9}\\2x-y=\dfrac{18}{11}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-\dfrac{18}{11}\\x+3\left(2x-\dfrac{18}{11}\right)=\dfrac{8}{9}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{82}{99}\\y=\dfrac{2}{99}\end{matrix}\right.\)
YN
8 tháng 2 2023
Gõ đề có sai không ạ?
\(\left\{{}\begin{matrix}\sqrt{3+2x^2y-x^4y^2}+x^4\left(1-2x^2\right)=y^4\\1+\sqrt{1+\left(x-y\right)^2}=x^3\left(x^3-x+2y^2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{4-\left(1-x^2y\right)^2}=2x^6-x^4+y^4\\-\sqrt{1+\left(x-y\right)^2}=1-x^6+x^4-2x^3y^2\end{matrix}\right.\)
Cộng theo vế HPT2
\(\sqrt{4-\left(1-x^2y\right)^2}-\sqrt{1+\left(x-y\right)^2}=\left(x^3-y^2\right)^2+1\)
\(\Leftrightarrow\sqrt{4-\left(1-x^2y\right)^2}=\sqrt{1+\left(x-y\right)^2}+\left(x^3-y^2\right)^2+1\) (1)
Có:
\(\left\{{}\begin{matrix}\sqrt{4-\left(1-x^2y\right)^2}\le2\\\sqrt{1+\left(x-y\right)^2}+\left(x^2-y^2\right)^2+1\ge2\end{matrix}\right.\)
\(\Rightarrow\) (1) xảy ra \(\Leftrightarrow\) \(\left\{{}\begin{matrix}\sqrt{4-\left(1-x^2y\right)^2}=2\\\sqrt{1+\left(x-y\right)^2}=1\\\left(x^3-y^2\right)^2=0\end{matrix}\right.\Leftrightarrow x=y=1\)
15 tháng 1 2023
a: =>2x-4+3+3y=-2 và 3x-6-2-2y=-3
=>2x+3y=-2+4-3=2-3=-1 và 3x-2y=-3+6+2=5
=>x=1; y=-1
b: =>x^2-x+xy-y=x^2+x-xy-y+2xy
=>-x-y=x-y và y^2+y-yx-x=y^2-2y+xy-2x-2xy
=>x=0 và y-x=-2y-2x
=>x=0 và y=0
a)\(3^x-y^3=1\)
Ta suy ra \(y^3+1⋮9\Rightarrow y^3:9\) dư -1
\(\Rightarrow y=9k+2\) hoặc \(y=9k+5\) hoặc \(y=9k+8\) (k nguyên dương) (1)
Mặt khác ta cũng có \(y^3+1⋮3\) nên \(y=3m+2\) (m nguyên dương)
Từ (1) và (2) suy ra vô nghiệm
Vậy pt có 2 nghiệm nguyên là (0;0) và (2;2)
b)Xét .... ta dc x=y=0 hoặc x=1 và y=2
c)Xét.... x=y=0 hoặc x=0 và y=-1 hoặc x=-1 và y=0 hoặc x=y=-1