cho a > b > 0 và a2 - 6b2 = -ab
tính M = 2ab / a2 - 3b2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
29 tháng 12 2023
Lời giải:
$a^2-2ab-3b^2\geq 0$
$\Leftrightarrow (a^2+ab)-(3ab+3b^2)\geq 0$
$\Leftrightarrow a(a+b)-3b(a+b)\geq 0$
$\Leftrightarrow (a+b)(a-3b)\geq 0$
$\Leftrightarrow a-3b\geq 0$ (do $a+b>0$ với mọi $a,b>0$)
$\Leftrightarrow a\geq 3b$
Xét hiệu:
$P-\frac{37}{3}=\frac{4a^2+b^2}{ab}-\frac{37}{3}$
$=\frac{12a^2+3b^2-37ab}{3ab}=\frac{(a-3b)(12a-b)}{3ab}\geq 0$ do $a\geq 3b>0$
$\Rightarrow P\geq \frac{37}{3}$
Vậy $P_{\min}=\frac{37}{3}$
CM
26 tháng 11 2018
Chọn đáp án D
Ta có
Suy ra
Từ giả thiết ta có f ' x + f ' ' x = 10 e x
Để phương trình f ' x + f ' ' x = 10 e x có nghiệm
⇔ Phương trình (*) có nghiệm
* Nếu b = 0 thì S = a 2 ≥ 10
* Nếu b ≠ 0 thì S = a 2 - 2 a b + 3 b 2 ≥ 10 . a b 2 - 2 . a b + 3 a b 2 + 1 .
Đặt t = a b t ∈ R , suy ra S ≥ 10 . t 2 - 2 t + 3 t 2 + 1 .
Xét hàm số f t = t 2 - 2 t + 3 t 2 + 1 trên R.
Ta có
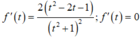
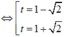
Bảng biến thiên:
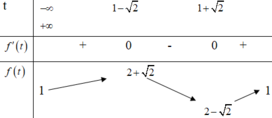
Quan sát bảng biến thiên ta thấy f t ≥ 2 - 2
TC
1
LT
0
NC
17 tháng 8 2020
a) Áp dụng Cauchy Schwars ta có:
\(M=\frac{a^2}{a+1}+\frac{b^2}{b+1}+\frac{c^2}{c+1}\ge\frac{\left(a+b+c\right)^2}{a+b+c+3}=\frac{9}{6}=\frac{3}{2}\)
Dấu "=" xảy ra khi: a = b = c = 1
NC
17 tháng 8 2020
b) \(N=\frac{1}{a}+\frac{4}{b+1}+\frac{9}{c+2}\ge\frac{\left(1+2+3\right)^2}{a+b+c+3}=\frac{36}{6}=6\)
Dấu "=" xảy ra khi: x=y=1
KM
0
KJ
2
4 tháng 9 2021
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
\(\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{3b^2}{27}=\dfrac{2c^2}{32}=\dfrac{a^2+3b^2-2c^2}{4+27-32}=\dfrac{-16}{-1}=16\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=64\\b^2=144\\c^2=256\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a=\pm8\\b=\pm12\\c=\pm16\end{matrix}\right.\)
Vậy \(\left(a;b;c\right)\in\left\{\left(8;12;16\right),\left(-8;-12;-16\right)\right\}\)
4 tháng 9 2021
Cách khác:
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k\\b=3k\\c=4k\end{matrix}\right.\)
Ta có: \(a^2+3b^2-2c^2=-16\)
\(\Leftrightarrow4k^2+27k^2-32k^2=-16\)
\(\Leftrightarrow k^2=16\)
Trường hợp 1: k=4
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=8\\b=3k=12\\c=4k=16\end{matrix}\right.\)
Trường hợp 2: k=-4
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=-8\\b=3k=-12\\c=4k=-16\end{matrix}\right.\)