trong các hình thang có 3 cạnh bằng nhau tìm hình thang có diện tích lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


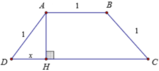
Chọn đáp án C
Phương pháp
Sử dụng công thức tính chu vi hình thang, diện tích hình thang và áp dụng định lý Pi-ta-go.
Xét hàm số, tính giá trị lớn nhất.
Cách giải
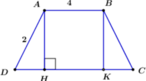
Gọi H là chân đường cao kẻ từ A đến CD ta có:
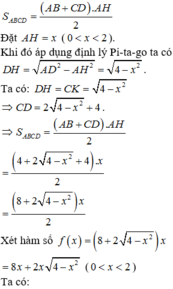
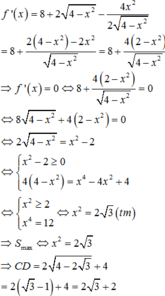
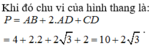

bài này sao khó vậy
mình không làm được đâu
nhưng cô của mình cũng ra bài giống y hệt nếu có người trả lời thì thông báo cho mình biết nha
thank you very much

Đáp án D
Dựng A H ⊥ C D . Đặt D H = x 0 < x < 1
Ta có: D C = 2 x + 1 ⇒ A H = 1 − x 2
S A B C D = 1 + 2 x + 1 2 1 − x 2 = 1 + x 1 − x 2 = f x ⇒ f ' x = 1 − x 2 − 1 + x x 1 − x 2 = 0 ⇔ 1 − x 2 = 1 + x x ⇔ 2 x 2 + x − 1 = 0 ⇔ x = − 1 l o a i x = 1 2 ⇒ S m a x = f 1 2 = 3 3 4 ⇔ x = 1 2
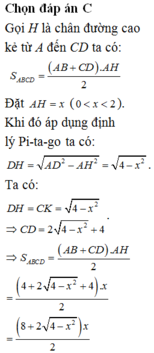
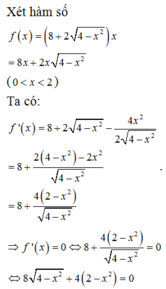

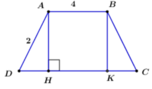


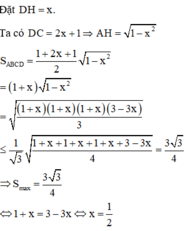
Giả sử hình có hình thang ABCD mà AD = AB = BC = a
Từ B kẻ BE // AD => DE = BE = a
Gọi BH là đường cao của hình thang => HE = HC đặt HE = x. Vậy ta có \(BH=\sqrt{a^2-x^2}\)
Diện tích hình thang ABCD là:
\(S=\frac{AB+DC}{2}.BH=\frac{a+a+2x}{2}.\sqrt{a^2-x^2}\)
\(=\left(a+x\right)\sqrt{a^2-x^2}=\sqrt{\left(a+x\right)^2\left(a^2-x^2\right)}\)
\(=\sqrt{27\left(a-x\right).\frac{a+x}{3}.\frac{a+x}{3}.\frac{a+x}{3}}\)(1)
Muốn S lớn nhất thì vế phải của (1) lớn nhất. Mặt khác ta có:
\(\left(a-x\right)+\frac{a+x}{3}+\frac{a+x}{3}+\frac{a+x}{3}=2a\)không đổi, nên S lớn nhất khi \(a-x=\frac{a+x}{3}\Rightarrow a=2x\)
Như vậy hình thang có ba cạnh bằng nhau thì hình thang có một góc bằng 600 có diện tích lớn nhất.