Cho tam giác ABC có diện tích = 180cm2.Trên cạnh BC lấy điểm K sao cho BK =1/3 BC, H là trung điểm của AC, nối A với K, Kvới H, G là trung điểm của KH. Tính diện tích AKG
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
11 tháng 11 2016
Bài này chỉ cần dùng tỉ lệ diện tích thông qua tỉ lệ cạnh và chiều cao. Ta có hình vẽ:
Do tam giác ABC và AKC có chung chiều cao nên \(\frac{S_{AKC}}{S_{ABC}}=\frac{KC}{BC}=\frac{2}{3}\Rightarrow S_{AKC}=\frac{2}{3}\times180=120\left(cm^2\right).\)
Do H là trung điểm AC, hai tam giác KAH và KCH chung chiều cao nên \(\frac{S_{AKH}}{S_{AKC}}=\frac{1}{2}\Rightarrow S_{AKH}=\frac{1}{2}\times120=60\left(cm^2\right)\)
Do G là trung điểm KH, hai tam giác AKH và AGH chung chiều cao nên \(\frac{S_{AKG}}{S_{AHK}}=\frac{1}{2}\Rightarrow S_{AKG}=\frac{1}{2}\times60=30\left(cm^2\right).\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 6 2023
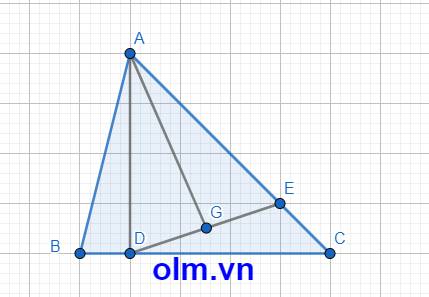
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%