tính diện tích tam giác ABC nếu biết AB = AC =20cm, BC = 25 cm.
Giúp mk zới cần gấp ạk
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
22 tháng 4 2017
A B C 8 cm 6 cm 10 cm H
\(\text{Ta có: BC là cạnh lớn nhất }\)
\(\text{Mà }\sqrt{AB^2+AC^2}=\sqrt{8^2+6^2}=10\)
\(\text{Vậy tam giác ABC là tam giác vuông tại A}\)
b.Anh tính theo 2 cách nhé nhưng em chọn cách nào cx dc..
\(\text{C1}:\)\(\text{Áp dụng định lý PTG vào tam giác AHB}\)
\(AH=\sqrt{AB^2-HB^2}=\sqrt{8^2-\left(6,4\right)^2}=4,8\)
\(\text{Vậy S ABC là}:\frac{1}{2}.AH.BC=\frac{1}{2}.4,8.10=24\)
\(\text{C2}\)
\(\text{C2 đơn giản hơn k cần dùng câu b cx dc}\)
Vì ABC là tam giác vuông nên
\(\text{S ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.6.8=24\)
BV
20 tháng 2 2020
Lời giải:
Sử dụng tính chất đường phân giác:
ABAC=BDDC=1520=34(1)ABAC=BDDC=1520=34(1)
Áp dụng định lý Pitago cho tam giác vuông ABCABC:
AB2+AC2=BC2=(BD+DC)2=352=1225(2)AB2+AC2=BC2=(BD+DC)2=352=1225(2)
Từ (1);(2)⇒AB3=AC4⇒AB29=AC216=AB2+AC29+16=122525=49(1);(2)⇒AB3=AC4⇒AB29=AC216=AB2+AC29+16=122525=49
⇒{AB2=49.9AC2=49.16⇒AB=21;AC=28⇒{AB2=49.9AC2=49.16⇒AB=21;AC=28 (cm)
CM
27 tháng 8 2018
Vì △ ABD và △ ABC có chung đường cao kẻ từ đỉnh A nên:
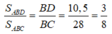
Vậy: S A B D = 3/8.S
S A D C = S A B C - S A B D = S - 3/8.S = 8/8.S - 3/8.S = 5/8.S
Vì DE // AB và AD là đường phân giác góc A nên AE = DE
Ta có: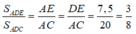 
Vậy: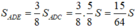 
Ta có: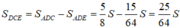 
12 tháng 10 2015
a) Áp dụng: Diện tích của một tam giác bằng nửa tích của 2 cạnh nhân với sin của góc nhọn tạo bởi các đường thẳng chứa 2 cạnh ấy
Cách 1: Dùng công thức Heron
Đặt
BC=a; AC=b; AB=c
\(p=\dfrac{a+b+c}{2}\)
\(S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
Cách 2
A B C H
Dựng đường cao AH
tg ABC có AB=AC => tg ABC cân
=> AH là trung tuyến (trong tg cân đường cao xp từ đỉnh tg cân đồng thời là đường trung tuyến)
=> \(HB=HC=\dfrac{BC}{2}=\dfrac{25}{2}=12,5cm\)
Xét tg ABH có
\(AH=\sqrt{AB^2-HB^2}\)
\(\Rightarrow S_{ABC}=\dfrac{BC.AH}{2}\)