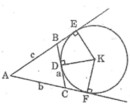
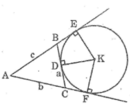
Cho tam giác ABC nhọn với BC = a, AC - b, AB = c và nửa chu vi p. Đường tròn bàng tiếp góc
A là đường tròn tiếp xúc cạnh BC và tiếp xúc với các tia đối tia BA, CA. Gọi (Ia, ra) là đường tròn
bàng tiếp góc A, đường tròn này tiếp xúc với BC, CA, AB lần lượt tại M, N, P .
(a) Tính AN, AP, BM, BP, CM, CN theo a, b, c?
(b) Chứng minh rằng 1
ra
=
1 p
cot
A 2
.
(c) Chứng minh rằng S = ra(p - a), ở đây S là diện tích tam giác.
(d) Gọi (Ib, rb), (Ic, rc) lần lượt là các đường tròn bàng tiếp góc B, C. Chứng minh rằng 1/ra+1/ rb+1 r/c=1/ r
và ra + rb + rc = 4R + r, ở đây R, r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp của
tam giác.
(e) Chứng minh rằng R ≥ 2r
các bạn giúp mình với