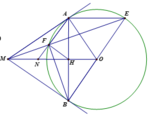
Cho đường tròn tâm O. Từ điểm E ở ngoài đường tròn kẻ hai tiếp tuyến EM và EN (M và N là các tiếp điểm). OE cắt MN tại H
a/ Chứng minh 4 điểm E, M, O, N cùng thuộc một đường tròn, xác định tâm và bán kính của đường tròn đó.
b/ Chứng minh OE vuông góc với MN.

a/
Ta có
\(\widehat{EMO}=\widehat{ENO}\) => EMON là tứ giác nội tiếp
=> E; M; O; N cùng nằm trên 1 đường tròn có tâm là trung điểm của EO và bán kính là EO/2
b/
Xét tg vuông EMO và tg vuông ENO có
EM=EN (hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
EO chung
=> tg EMO = tg ENO (Hai tg vuông có cạnh huyền và cạnh góc vuông bằng nhau)
=> \(\widehat{MEO}=\widehat{NEO}\)
Xét tg EMN có
EM=EN (cmt) => tg EMN cân tại E
\(\widehat{MEO}=\widehat{NEO}\) (cmt) => OE là phân giác của \(\widehat{MEN}\)
=> \(OE\perp MN\) (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao)
a, Xét tứ giác EMON có ^EMO + ^ENO = 1800
mà 2 góc này đối
Vậy tứ giác EMON nt 1 đường tròn hay E;M;O;N thuộc 1 đường tròn
bán kính là OE/2
b, Vì ME = MN ( 2 tiếp tuyến cắt nhau )
OM = ON
Vậy EO là đường trung trực đoạn MN
Vậy OE vuông MN