Chứng minh rằng với mọi giá trị của tham số m, hàm số y = x3 – mx2 – 2x + 1 luôn luôn có một điểm cực đại và một điểm cực tiểu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TXĐ: D = R
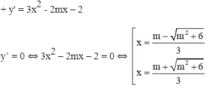
+ y’’ = 6x – 2m.
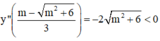
⇒ 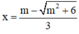 là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.
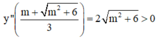
⇒ 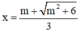 là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.

y’ = 3x2 – 2mx – 2 , ∆’ = m2 + 6 > 0 nên y’ = 0 có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.

y’ = 3x2 – 2mx – 2 , ∆’ = m2 + 6 > 0 nên y’ = 0 có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
Vậy hàm số luôn có một cực đại và một cực tiểu.

Chọn A
[Phương pháp trắc nghiệm]
y ' = 3 x 2 + 2 m x + 7
![]()
Bấm máy tính
![]()
![]()
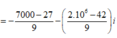
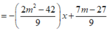
Đường thẳng đi qua 2 điểm cực trị là

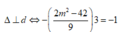
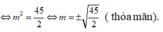

y′ = 3 x 2 − 2(m + 4)x – 4
∆ ′ = m + 4 2 + 12
Vì ∆ ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.

Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
(I) sai. Ví dụ hàm số 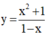 có đồ thị hàm số như sau:
có đồ thị hàm số như sau:
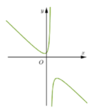 õ ràng
õ ràng ![]()
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số ![]() => Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là:
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: ![]() luôn song song với trục hoành.
luôn song song với trục hoành.
Vậy (III) đúng.

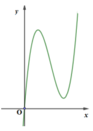

Để đồ thị hàm số có 2 điểm cực trị thì
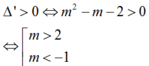
Khi đó, do a = 1 3 > 0 nên hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương . Đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất là x = 0 1 và hai cực trị x 1 ; x 2 x 1 < x 1 thỏa mãn: 0 < x 1 < x 2 2
Ta có:
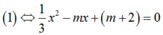
hoặc là vô nghiệm hoặc là có nghiệm kép x = 0
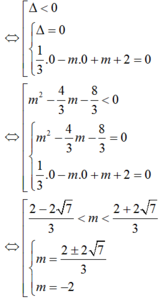
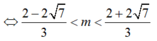
Kết hợp điều kiện ta có:
m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
Chọn: A

a) y = x 3 − (m + 4) x 2 − 4x + m
⇔ ( x 2 − 1)m + y − x 3 + 4 x 2 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
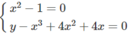
Giải hệ, ta được hai nghiệm:
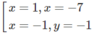
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
b) y′ = 3 x 2 − 2(m + 4)x – 4
Δ′ = ( m + 4 ) 2 + 12
Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c) Học sinh tự giải.
d) Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
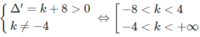

Chọn A
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 ) .
Hàm số có hai cực trị => y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=> ( 3 m ) 2 - 3 . 3 ( m 2 - 1 ) > 0 <=> 9 > 0 đúng với mọi m. Ta có điểm cực đại là B(m - 1; -2m + 2) và cực tiểu là C(m + 1; -2m - 2)
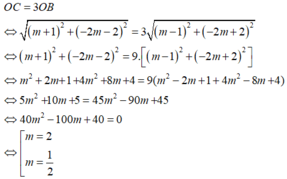
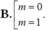
y= x3-mx2-2x+1
y'=3x^2-2mx-2
PT y'=3x^2-2mx-2=0 có delta'=m^2+6>0 với mọi m
nên có 2 nghiệm phân biệt.
vậy hs có 1 cực đại và 1 cực tiểu