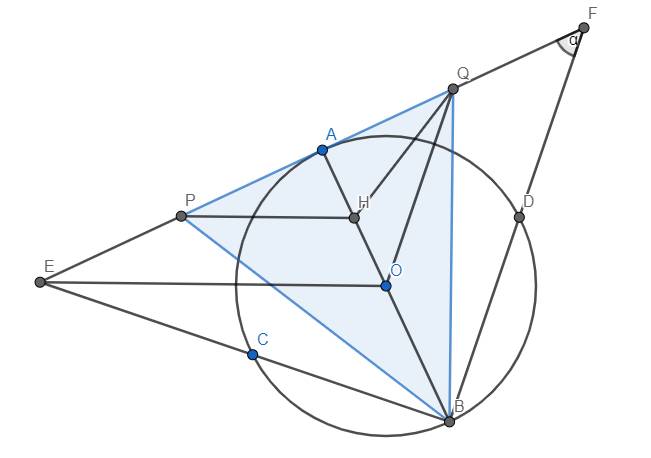
cho (O) đường kính AB cố định và đường kính CD thay đổi không trùng với AB.Tiếp tuyến tại A của (O) cắt các đường thẳng BC và BD lần lượt tại E và F.Gọi P và Q lần lượt là trung điểm của AE và AF.
1.Gọi H là trực tâm của tam giác BPQ.chứng min H là trung điểm của OA.
2.Xác định vị trí của CD để tam giác BPQ có diện tích nhỏ nhất