5x(2x-1)3-36=99
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 8 2023
3) \(...\Rightarrow2^x\left(2^3+1\right)=36\)
\(\Rightarrow2^x.9=36\)
\(\Rightarrow2^x=4\)
\(\Rightarrow2^x=2^2\Rightarrow x=2\)
4) \(...\Rightarrow4^{x+1}-4^x=12\)
\(\Rightarrow4^x\left(4-1\right)=12\)
\(\Rightarrow4^x.3=12\)
\(\Rightarrow4^x=4=4^1\Rightarrow x=1\)
5) \(...\Rightarrow5^{x+1}\left(5^2-1\right)=3000\)
\(\Rightarrow5^{x+1}.24=3000\)
\(\Rightarrow5^{x+1}=125\)
\(\Rightarrow5^{x+1}=5^3\)
\(\Rightarrow x+1=3\)
\(\Rightarrow x=2\)
6) Bạn xem lại đề
21 tháng 8 2023
a. \(2^x.2^3+2^x=36\)
\(2^x\left(2^3+1\right)=36\)
\(2^x.9=36\)
\(2^x=4\Rightarrow x=2\)
b. \(4^x.4^1-\left(2^2\right)^x=12\)
\(4^x.4-4^x=12\)
\(4^x\left(4-1\right)=12\)
\(4^x.3=12\)
\(4^x=4\)
x = 1
c. \(5^x.5^3-5^x.5^1=3000\)
\(5^x\left(5^3-5^1\right)=3000\)
\(5^x.120=3000\)
\(5^x=25\)
x = 2
d. \(4^{x+1}=2^{2x}\)
\(4^x.4=\left(2^2\right)^x\)
\(4^x.4=4^x\)
Có vẻ như câu 4 này để bài thiếu
16 tháng 6 2023
1: \(=6x^2+2x-15x-5-x^2+6x-9+4x^2+20x+25-27x^3-27x^2-9x-1\)
=-27x^3-18x^2+4x+10
2: =4x^2-1-6x^2-9x+4x+6-x^3+3x^2-3x+1+8x^3+36x^2+54x+27
=7x^3+37x^2+46x+33
5:
\(=25x^2-1-x^3-27-4x^2-16x-16-9x^2+24x-16+\left(2x-5\right)^3\)
\(=8x^3-60x^2+150-125+12x^2-x^3+8x-60\)
=7x^3-48x^2+8x-35
LP
1
TM
17 tháng 12 2016
Câu 1:
\(x^4+5x^3-12x^2+5x+1=x^4+7x^3+x^2-2x^3-14x^2-x+x^2+7x+1\)
\(=\left(x^4+7x^3+x^2\right)-\left(2x^3+14x^2+x\right)+\left(x^2+7x+1\right)\)
\(=x^2\left(x^2+7x+1\right)-2x\left(x^2+7x+1\right)+\left(x^2+7x+1\right)\)
\(=\left(x^2-2x+1\right)\left(x^2+7x+1\right)\)
\(=\left(x-1\right)^2\left(x^2+7x+1\right)\)
Câu 2:
\(\left(x-3\right)\left(x-5\right)\left(x-6\right)\left(x-10\right)-24x^2=x^4-24x^3+203x^2-720x+900-24x^2\)
\(=x^4-24x^3+179x^2-720x+900\)
\(=\left(x^4-7x^3+30x^2\right)-\left(17x^3-119x^2+510x\right)+\left(30x^2-210x+900\right)\)
\(=x^2\left(x^2-7x+30\right)-17x\left(x^2-7x+30\right)+30\left(x^2-7x+30\right)\)
\(=\left(x^2-17x+30\right)\left(x^2-7x+30\right)\)
\(=\left(x^2-2x-15x+30\right)\left(x^2-7x+30\right)\)
\(=\left[x\left(x-2\right)-15\left(x-2\right)\right]\left(x^2-7x+30\right)\)
\(=\left(x-15\right)\left(x-2\right)\left(x^2-7x+30\right)\)
Câu 3:
\(2x^3+11x^2+3x-36=\left(2x^3+14x^2+24x\right)-\left(3x^2+21x+36\right)\)
\(=2x\left(x^2+7x+12\right)-3\left(x^2+7x+12\right)\)
\(=\left(2x-3\right)\left(x^2+7x+12\right)\)
\(=\left(2x-3\right)\left(x^2+3x+4x+12\right)\)
\(=\left(2x-3\right)\left[x\left(x+3\right)+4\left(x+3\right)\right]\)
\(=\left(2x-3\right)\left(x+3\right)\left(x+4\right)\)
4 tháng 1 2022
Bài 1:
a: \(=6x^3-10x^2+6x\)
b: \(=-2x^3-10x^2-6x\)
Bài 4:
a: =>3x+10-2x=0
=>x=-10
c: =>3x2-3x2+6x=36
=>6x=36
hay x=6
4 tháng 1 2022
Bài 1:
\(a,=6x^3-10x^2+6x\\ b,=-2x^3-10x^2-6x\)
Bài 4:
\(a,\Leftrightarrow3x+10-2x=0\Leftrightarrow x=-10\\ b,\Leftrightarrow x\left(2x^2+9x-5\right)-\left(2x^3+9x^2+x+4,5\right)=3,5\\ \Leftrightarrow2x^3+9x^2-5x-2x^3-9x^2-x-4,5=3,5\\ \Leftrightarrow-6x=8\Leftrightarrow x=-\dfrac{4}{3}\\ c,\Leftrightarrow3x^2-3x^2+6x=36\Leftrightarrow x=6\)
Bài 1:
\(a,=7xy\left(2x-3y+4xy\right)\\ b,=x\left(x+y\right)-5\left(x+y\right)=\left(x-5\right)\left(x+y\right)\\ c,=\left(x-y\right)\left(10x+8\right)=2\left(5x+4\right)\left(x-y\right)\\ d,=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\\ =2x\left(4x+2\right)=4x\left(2x+1\right)\\ e,=5\left[\left(x-y\right)^2-4z^2\right]=5\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=x^2+8x-x-8=\left(x+8\right)\left(x-1\right)\\ g,\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\\ h,=x^2+3x+x+3=\left(x+3\right)\left(x+1\right)\)
YN
3 tháng 7 2021
\(1.\)
\(4x^2-4x-3\)
\(=4x^2-2x+6x-3\)
\(=2x\left(2x-1\right)+3\left(2x-1\right)\)
\(=\left(2x+3\right)\left(2x-1\right)\)
\(2.\)
\(2x^2-5x-3\)
\(=2x^2-6x+x-3\)
\(=2x\left(x-3\right)+\left(x-3\right)\)
\(=\left(2x+1\right)\left(x-3\right)\)
\(3.\)
\(3x^2-5x-2\)
\(=3x^2+x-6x-2\)
\(=x\left(3x+1\right)-2\left(3x+1\right)\)
\(=\left(3x+1\right)\left(x-2\right)\)
\(4.\)
\(2x^2+5x+2\)
\(=2x^2+4x+x+2\)
\(=2x\left(x+2\right)+\left(x+2\right)\)
\(=\left(2x+1\right)\left(x+2\right)\)
YN
3 tháng 7 2021
\(5.\)
\(6x^2-x-1\)
\(=6x^2-3x+2x-1\)
\(=2x\left(3x+1\right)-\left(3x+1\right)\)
\(=\left(2x-1\right)\left(3x+1\right)\)
\(6.\)
\(6x^2-6x-3\)
\(=3\left(2x^2-2x-1\right)\)
\(7.\)
\(15x^2-2x-1\)
\(=15x^2+3x-5x-1\)
\(=3x\left(5x+1\right)-1\left(5x+1\right)\)
\(=\left(5x+1\right)\left(3x-1\right)\)
\(8.\)
\(x^4-13x^2+36\)
\(=\left(x-3\right)\left(x^3+3x^2-4x-12\right)\)
\(=\left(x-3\right)\left(x-2\right)\left(x^2+5x+6\right)\)
\(=\left(x-3\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)\)
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
\(\begin{array}{l}a){\rm{ }}3{x^2}-{\rm{ }}3x\left( {x{\rm{ }}-{\rm{ }}2} \right){\rm{ }} = {\rm{ }}36\\ \Leftrightarrow 3{x^2}-{\rm{ [}}3x.x + 3x.( - 2)] = 36\\ \Leftrightarrow 3{x^2} - (3{x^2} - 6x) = 36\\ \Leftrightarrow 3{x^2} - 3{x^2} + 6x = 36\\ \Leftrightarrow 6x = 36\\ \Leftrightarrow x = 36:6\\ \Leftrightarrow x = 6\end{array}\)
Vậy x = 6
\(\begin{array}{l}b){\rm{ }}5x\left( {4{x^2}-{\rm{ }}2x{\rm{ }} + {\rm{ }}1} \right){\rm{ }}-{\rm{ }}2x\left( {10{x^2}-{\rm{ }}5x{\rm{ }} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }} - 36\\ \Leftrightarrow 5x.4{x^2} + 5x.( - 2x) + 5x.1 - [2x.10{x^2} + 2x.( - 5x) + 2x.2] = - 36\\ \Leftrightarrow 20{x^3} - 10{x^2} + 5x - (20{x^3} - 10{x^2} + 4x) = - 36\\ \Leftrightarrow 20{x^3} - 10{x^2} + 5x - 20{x^3} + 10{x^2} - 4x = - 36\\ \Leftrightarrow (20{x^3} - 20{x^3}) + ( - 10{x^2} + 10{x^2}) + (5x - 4x) = - 36\\ \Leftrightarrow x = - 36\end{array}\)
Vậy x = -36
PN
13 tháng 6 2019
a) \(3\left(2x-1\right)\left(3x-1\right)-\left(2x-3\right)\left(9x-1\right)-3=-3\)
\(\Leftrightarrow18x^2-15x+3-18x^2+29x-3-3=-3\)
\(\Leftrightarrow14x=0\)
\(\Leftrightarrow x=0\)
Vậy pt có nghiệm duy nhất x = 0.
b) \(\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(6x-5\right)=\left(x+2\right)-\left(x-5\right)\)
\(\Leftrightarrow6x^2+19x-7-6x^2-x+5=7\)
\(\Leftrightarrow18x-2=7\)
\(\Leftrightarrow18x=9\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy pt có nghiệm duy nhất \(x=\frac{1}{2}\)
c) \(\left(6x-2\right)^2+\left(5x-2\right)^2-4\left(3x-1\right)\left(5x-2\right)=0\)
\(\Leftrightarrow36x^2-24x+4+25x^2-20x+4-60x^2+33x-8=0\)
\(\Leftrightarrow x^2-11x=0\)
\(\Leftrightarrow x\left(x-11\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=11\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{0;11\right\}\)
d) \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\)
\(\Leftrightarrow x^2-6x+9-x^2-4x+32=1\)
\(\Leftrightarrow41-10x=1\)
\(\Leftrightarrow-10x=40\)
\(\Leftrightarrow x=-4\)
Vậy pt có nghiệm duy nhất x = -4.
e) \(3\left(x+2\right)^2+\left(2x-1\right)^2-7\left(x+3\right)\left(x-3\right)=36\)
\(\Leftrightarrow3\left(x^2+4x+4\right)+4x^2-4x+1-7x^2+36=36\)
\(\Leftrightarrow3x^2+12x+12+4x^2-4x+1-7x^2=0\)
\(\Leftrightarrow8x=-13\)
\(\Leftrightarrow x=-\frac{13}{8}\)
Vậy pt có nghiệm duy nhất \(x=-\frac{13}{8}\)
20 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
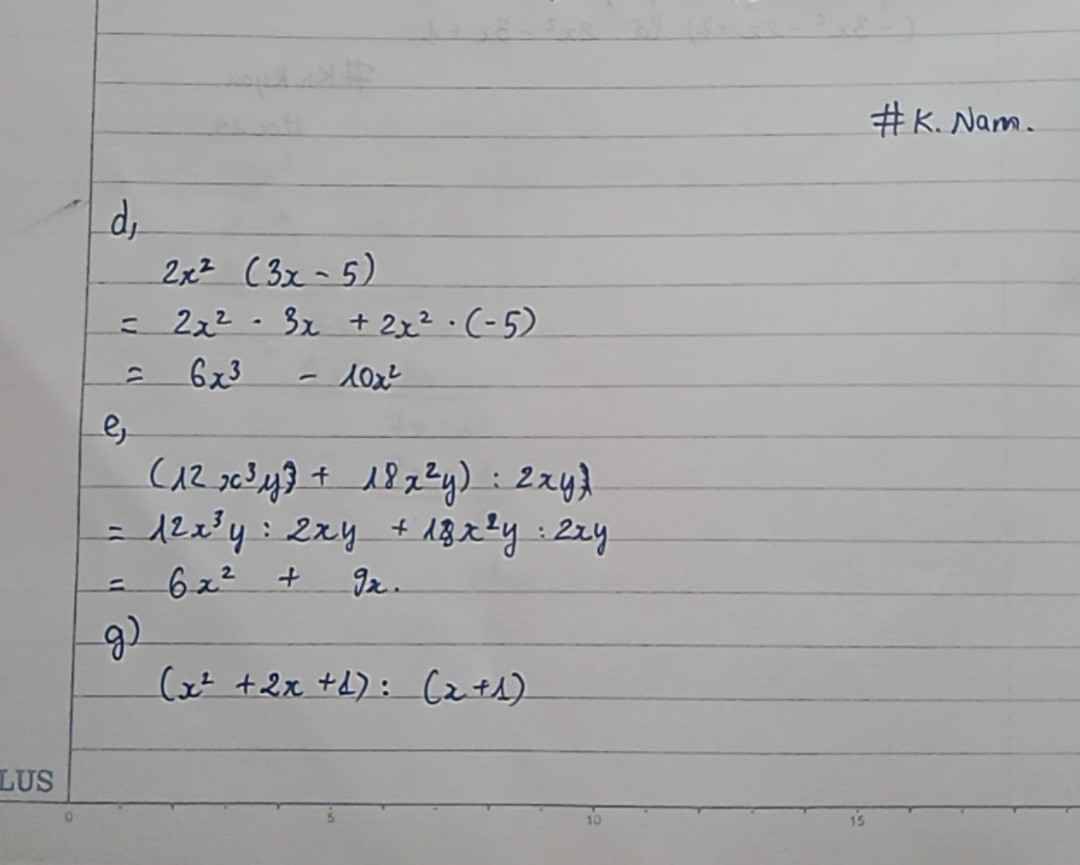
*Máy tớ cam hơi mờ, cậu thông cảm ._.*
Cậu viết lại rõ đề câu c, nhé.
CN
0
5x(2x-1)3-36=99
5x(2x-1)3 =99+36
5x(2x-1)3 = 125
(2x-1)3 =125:5
(2x-1)3 = 25
(2x-1)3 =53
\(\Rightarrow\)2x-1 =5
2x =5+1
2x =6
x= 6:2
x= 3