Cho a2+b2+c2=1
Tìm GTNN của biểu thức \(P=a+b+c+\frac{1}{abc}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
12 tháng 8 2023
Ta có:
P = a + b + c ≤ a + b + a + b = 2(a + b) ≤ 2(-1) = -2
Ta cũng có:
P = a + b + c ≤ a + b + c - 2abc ≥ a + b + c - 2(-1)(-1)(-1) = -3
Vậy GTNN của P = -3 và GTLN của P = -2.
EC
2
4 tháng 7 2021
áp dụng BDT AM-GM
\(=>a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\)
\(=>1\ge3\sqrt[3]{\left(abc\right)^2}=>1\ge27\left(abc\right)^2\)\(=>27\left(abc\right)^2\le1=>3\left(abc\right)^2\le\dfrac{1}{9}=>\left(abc\right)^2\le\dfrac{1}{27}=>abc\le\dfrac{1}{3\sqrt{3}}\)
\(=>\dfrac{8}{9abc}\ge\dfrac{8}{9.\dfrac{1}{3\sqrt{3}}}=\dfrac{8\sqrt{3}}{3}\)
\(S=a+b+c+\dfrac{1}{abc}=a+b+c+\dfrac{1}{9abc}+\dfrac{8}{9abc}\)
\(=>a+b+c+\dfrac{1}{9abc}\ge4\sqrt[4]{\dfrac{1}{9}}=\dfrac{4}{\sqrt{3}}\)
\(=>S\ge\dfrac{4}{\sqrt{3}}+\dfrac{8}{\sqrt{3}}=4\sqrt{3}\)
dấu"=" xyar ra<=>a=b=c=\(\dfrac{1}{\sqrt{3}}\)
4 tháng 7 2021
Các bn mà cop thì nhớ giải thích giúp mik đoạn \(a^2+b^2+c^2\ge3\sqrt[3]{abc}\) với
AH
Akai Haruma
Giáo viên
2 tháng 5 2023
Lời giải:
$P=\frac{a^2b^2+b^2c^2+c^2a^2}{abc}$
Áp dụng BĐT AM-GM, dạng $(x+y+z)^2\geq 3(xy+yz+xz)$ ta có:
$(a^2b^2+b^2c^2+c^2a^2)^2\geq 3(a^2b^4c^2+a^4b^2c^2+a^2b^2c^4)$
$=3a^2b^2c^2(a^2+b^2+c^2)=3a^2b^2c^2$
$\Rightarrow a^2b^2+b^2c^2+c^2a^2\geq \sqrt{3}abc$
$\Rightarrow P=\frac{a^2b^2+b^2c^2+c^2a^2}{abc}\geq \sqrt{3}$
Vậy $P_{\min}=\sqrt{3}$. Giá trị này đạt tại $a=b=c=\frac{1}{\sqrt{3}}$
CM
11 tháng 3 2018
Ta có
D = a ( b 2 + c 2 ) – b ( c 2 + a 2 ) + c ( a 2 + b 2 ) – 2 a b c = a b 2 + a c 2 – b c 2 – b a 2 + c a 2 + c b 2 – 2 a b c = ( a b 2 – a 2 b ) + ( a c 2 – b c 2 ) + ( a 2 c – 2 a b c + b 2 c ) = a b ( b – a ) + c 2 ( a – b ) + c ( a 2 – 2 a b + b 2 ) = - a b ( a – b ) + c 2 ( a – b ) + c ( a – b ) 2 = ( a – b ) ( - a b + c 2 + c ( a – b ) ) = ( a – b ) ( - a b + c 2 + a c – b c ) = ( a – b ) [ ( - a b + a c ) + ( c 2 – b c ) ]
= (a – b)[a(c – b) + c(c – b)]
= (a – b)(a + c)(c – b)
Với a = 99; b = -9; c = 1, ta có
D = (99 - (-9))(99 + 1) (1 - (-9)) = 108.100.10 = 108000
Đáp án cần chọn là: B
10 tháng 6 2021
mới ăn miếng cơm cà ngon nhức nách luôn ai thèm cơm cà không điểm danh nào
NC
17 tháng 8 2020
a) Áp dụng Cauchy Schwars ta có:
\(M=\frac{a^2}{a+1}+\frac{b^2}{b+1}+\frac{c^2}{c+1}\ge\frac{\left(a+b+c\right)^2}{a+b+c+3}=\frac{9}{6}=\frac{3}{2}\)
Dấu "=" xảy ra khi: a = b = c = 1
NC
17 tháng 8 2020
b) \(N=\frac{1}{a}+\frac{4}{b+1}+\frac{9}{c+2}\ge\frac{\left(1+2+3\right)^2}{a+b+c+3}=\frac{36}{6}=6\)
Dấu "=" xảy ra khi: x=y=1
LV
1
16 tháng 7 2021
Áp dụng bất đẳng thức cosi ta có:
`a^2+b^2>=2ab`
`b^2+c^2>=2bc`
`c^2+a^2>=2ca`
`=>2(a^2+b^2+c^2)>=2ab+2bc+2ca`
`=>3(a^2+b^2+c^2)>=a^2+b^2+c^2+2ab+2bc+2ca`
`=>3A>=(a+b)^2=1`
`=>A>=1/3`
Dấu "=" xảy ra khi `a=b=c=1/3`
11 tháng 6 2023
\(\)Ta có: \(a+b+c=0 \Rightarrow b+c=-a \Rightarrow (b+c)^2=(-a)^2 \Leftrightarrow b^2+c^2+2bc=a^2 \Leftrightarrow a^2-b^2-c^2=2bc\)
Tương tự: \(b^2-c^2-a^2=2ca;c^2-a^2-b^2=2ab\)
\(P=...=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2bc}=\dfrac{a^3+b^3+c^3}{2abc}=\dfrac{3abc}{2abc}=\dfrac{3}{2}\)
----
Bổ đề \(a+b+c=0 \Leftrightarrow a^3+b^3+c^3\)
Ở đây ta c/m chiều thuận:
Với \(a+b+c=0 \Leftrightarrow a+b=-c \Rightarrow (a+b)^3=(-c)^3 \Leftrightarrow a^3+b^3+3ab(a+b)=-c^3 \Leftrightarrow a^3+b^3+c^3=3abc(QED)\)
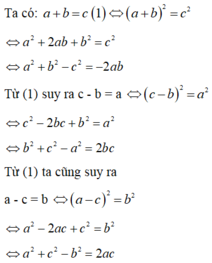
(Đề có cho \(a,b,c\) dương không bạn? Nếu có thì ta làm như sau:)
Dự đoán \(P\) đạt GTNN tại \(a=b=c=\frac{1}{\sqrt{3}}\), nghĩa là \(\frac{1}{abc}=3\sqrt{3}\).
Vậy ta tách: \(P=9a+9b+9c+\frac{1}{abc}-8\left(a+b+c\right)\)
Áp dụng BĐT Cauchy và BĐT \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\) ta có:
\(P\ge4.\sqrt[4]{9^3}-8\sqrt{3}=4\sqrt{3}\). Đẳng thức xảy ra tại \(a=b=c=\frac{1}{\sqrt{3}}\)