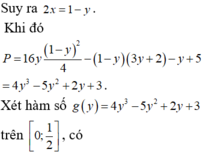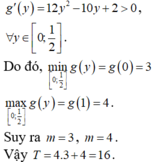tìm giá trị lớn nhất của (1-x)(2-y)(4x+3y) với 0<x<1 , 0<2<y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
0
CL
3
9 tháng 12 2017
\(x^2+2xy+4x+4y+3y^2+3=0\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(4x+4y\right)+4+2y^2-1=0\)
\(\Leftrightarrow\left(x+y\right)^2+4\left(x+y\right)+4=1-2y^2\)
\(\Leftrightarrow\left(x+y+2\right)^2=1-2y^2\)
Do \(VP=1-2y^2\le1\forall y\) nên \(VT=\left(x+y+2\right)^2\le1\)
\(\Leftrightarrow-1\le x+y+2\le1\)
\(\Leftrightarrow-1+2015\le x+y+2+2015\le1+2015\)
\(\Leftrightarrow2014\le x+y+2017\le2016\)
Hay \(2014\le B\le2016\)
8 tháng 12 2016
- \(B=\left(4x^2+3y\right)\left(4y^2+3x\right)+25xy=16x^2y^2+12\left(x^3+y^3\right)+34xy\)
\(=16x^2y^2+12\left(x+y\right)\left(x^2-xy+y^2\right)+34xy\)
\(=16x^2y^2+12\left[\left(x+y\right)^2-2xy\right]+22xy\)
\(=16x^2y^2-2xy+12\)
Đặt \(t=xy\) thì \(B=16t^2-2t+12=16\left(t-\frac{1}{16}\right)^2+\frac{191}{16}\ge\frac{191}{16}\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}x+y=1\\xy=\frac{1}{16}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{2+\sqrt{3}}{4}\\y=\frac{2-\sqrt{3}}{4}\end{cases}}\) hoặc \(\hept{\begin{cases}x=\frac{2-\sqrt{3}}{4}\\y=\frac{2+\sqrt{3}}{4}\end{cases}}\)
Vậy min B \(=\frac{191}{16}\) khi \(\left(x;y\right)=\left(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}\right);\left(\frac{2-\sqrt{3}}{4};\frac{2+\sqrt{3}}{4}\right)\)
- Như trên ta có : \(B=16\left(xy-\frac{1}{16}\right)^2+\frac{191}{16}\)
Mặt khác, áp dụng BĐT Cauchy , ta có : \(1=x+y\ge2\sqrt{xy}\Rightarrow xy\le\frac{1}{4}\)
Suy ra : \(B\le16\left(\frac{1}{4}-\frac{1}{16}\right)^2+\frac{191}{16}=\frac{25}{2}\)
Đẳng thức xảy ra khi x = y = 1/2
Vậy max B = 25/2 khi (x;y) = (1/2;1/2)
VP
2
KN
31 tháng 7 2020
a. \(-x^2+4x+y^2-12y+47\)
\(=-\left(x^2-4x-y^2+17y-47\right)\)
\(=-\left[x^2-4x+4-\left(y^2-12y+36\right)-15\right]\)
\(=-\left[\left(x-2\right)^2-\left(y-6\right)^2-15\right]\)
Vì \(\left(x-2\right)^2-\left(y-6\right)^2-15\ge-15\forall x\)
\(\Rightarrow-\left[\left(x-2\right)^2-\left(y-6\right)^2-15\right]\le15\)
Vậy GTLN của bt trên là 15 \(\Leftrightarrow x=2;y=6\)
KN
31 tháng 7 2020
b. \(-x^2-x-y^2-3y+13\)
\(=\frac{1}{4}\left(-4x^2-4x-4y^2-12y+52\right)\)
\(=\frac{1}{4}\left[-\left(2x+1\right)^2-\left(2y+3\right)^2+42\right]\)
Vì \(\frac{1}{4}\left[-\left(2x+1\right)^2-\left(2y+3\right)^2+42\right]\le42\forall x;y\)
\(\Rightarrow-\left(2x+1\right)^2-\left(2y+3\right)^2+42\le\frac{21}{2}\forall x;y\)
Vậy GTLN của bt trên là 21/2 \(\Leftrightarrow x=-\frac{1}{2};y=-\frac{3}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2023
\(M=6x^2+4y^2+6xy+\left(xy+\dfrac{4x}{y}\right)+\left(3xy+\dfrac{3y}{x}\right)+2022\)
\(M\ge3x^2+y^2+3\left(x+y\right)^2+2\sqrt{\dfrac{4x^2y}{y}}+2\sqrt{\dfrac{9xy^2}{x}}+2022\)
\(M\ge3\left(x^2+1\right)+\left(y^2+4\right)+3\left(x+y\right)^2+4x+6y+2015\)
\(M\ge6x+4y+3\left(x+y\right)^2+4x+6y+2015\)
\(M\ge3\left(x+y\right)^2+10\left(x+y\right)+2015\ge3.3^2+10.3+2015=2072\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(1;2\right)\)