Tính:\(\sqrt{\dfrac{9}{7-4\sqrt{3}}}-\sqrt{\dfrac{4}{7+4\sqrt{3}}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a) \sqrt{4x^2− 9} = 2\sqrt{x + 3}\)
\(ĐK:x\ge\dfrac{3}{2}\)
\(pt\Leftrightarrow4x^2-9=4\left(x+3\right)\)
\(\Leftrightarrow4x^2-9=4x+12\)
\(\Leftrightarrow4x^2-4x-21=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{22}}{2}\left(l\right)\\x=\dfrac{1+\sqrt{22}}{2}\left(tm\right)\end{matrix}\right.\)
\(b)\sqrt{4x-20}+3.\sqrt{\dfrac{x-5}{9}}-\dfrac{1}{3}\sqrt{9x-45}=4\)
\(ĐK:x\ge5\)
\(pt\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)
\(\Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\)
\(\Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)
\(c)\dfrac{2}{3}\sqrt{9x-9}-\dfrac{1}{4}\sqrt{16x-16}+27.\sqrt{\dfrac{x-1}{81}}=4\)
ĐK:x>=1
\(pt\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\)
\(\Leftrightarrow4\sqrt{x-1}=4\Leftrightarrow\sqrt{x-1}=1\)
\(\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)
\(d)5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)
\(ĐK:x\ge3\)
\(pt\Leftrightarrow3\sqrt{x-3}-\dfrac{14}{3}\sqrt{x-3}-7\sqrt{x^2-9}+6\sqrt{x^2-9}=0\)
\(\Leftrightarrow-\dfrac{5}{3}\sqrt{x-3}-\sqrt{x^2-9}=0\Leftrightarrow\dfrac{5}{3}\sqrt{x-3}+\sqrt{x^2-9}=0\)
\(\Leftrightarrow(\dfrac{5}{3}+\sqrt{x+3})\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}=0\) (vì \(\dfrac{5}{3}+\sqrt{x+3}>0\))
\(\Leftrightarrow x-3=0\Leftrightarrow x=3\left(nhận\right)\)

\(1,P=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\left(dkxd:x\ge0,x\ne9\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{2}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)-2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}-1-2\left(\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-3\sqrt{x}-2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\sqrt{x}-1-2\sqrt{x}+6}\)
\(=\dfrac{-x-3\sqrt{x}}{\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}}{-\sqrt{x}+5}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}}{5-\sqrt{x}}\)
\(=-\dfrac{x}{5-\sqrt{x}}\)
\(2,x=\sqrt{7+4\sqrt{3}}+\sqrt{7-4\sqrt{3}}\)
\(=\sqrt{\left(2+\sqrt{3}\right)^2}+\sqrt{\left(2-\sqrt{3}\right)^2}\)
\(=\left|2+\sqrt{3}\right|+\left|2-\sqrt{3}\right|\)
\(=2+\sqrt{3}+2-\sqrt{3}=4\)
\(x=4\Rightarrow P=-\dfrac{4}{5-\sqrt{4}}=\dfrac{-4}{5-2}=-\dfrac{4}{3}\)

\(A=\dfrac{\sqrt[4]{7\sqrt[3]{54}+15\sqrt[3]{128}}}{\sqrt[3]{\sqrt[4]{32}}+\sqrt[3]{9\sqrt[4]{162}}}\)
\(\Leftrightarrow A=\dfrac{\sqrt[4]{7\sqrt[3]{3^3.2}+15\sqrt[3]{4^3.2}}}{\sqrt[3]{\sqrt[4]{2^4.2}}+\sqrt[3]{9\sqrt[4]{3^4.2}}}\)
\(\Leftrightarrow A=\dfrac{\sqrt[4]{7.3\sqrt[3]{2}+15.4\sqrt[3]{2}}}{\sqrt[3]{2\sqrt[4]{2}}+\sqrt[3]{9.3\sqrt[4]{2}}}\)
\(\Leftrightarrow A=\dfrac{\sqrt[4]{21\sqrt[3]{2}+60\sqrt[3]{2}}}{\sqrt[3]{2\sqrt[4]{2}}+\sqrt[3]{3^3\sqrt[4]{2}}}\)
\(\Leftrightarrow A=\dfrac{\sqrt[4]{81\sqrt[3]{2}}}{\sqrt[3]{\sqrt[4]{2}}\left(\sqrt[3]{2}+3\right)}=\dfrac{3\sqrt[4]{\sqrt[3]{2}}}{\sqrt[3]{\sqrt[4]{2}}\left(\sqrt[3]{2}+3\right)}\)
\(\Leftrightarrow A=\dfrac{3}{\sqrt[3]{2}+3}\)

\(a,\dfrac{3}{\sqrt{7}-4}+\dfrac{4+\sqrt{7}}{3}\)
\(=\dfrac{9}{3\left(\sqrt{7}-4\right)}+\dfrac{\left(\sqrt{7}-4\right)\left(\sqrt{7}+4\right)}{3\left(\sqrt{7}-4\right)}\)
\(=\dfrac{9+7-16}{3\left(\sqrt{7}-4\right)}\)
\(=0\)
\(b,\left(\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{3}-1}+\dfrac{1}{\sqrt{3}+\sqrt{2}}\right):\dfrac{1}{2\sqrt{3}}\)
\(=\left[\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{3}+\sqrt{2}\right)}\right]\cdot2\sqrt{3}\)
\(=\left(\sqrt{2}+\dfrac{\sqrt{3}-\sqrt{2}}{3-2}\right)\cdot2\sqrt{3}\)
\(=\left(\sqrt{2}+\sqrt{3}-\sqrt{2}\right)\cdot2\sqrt{3}\)
\(=\sqrt{3}\cdot2\sqrt{3}\)
\(=6\)
#\(Toru\)

\(1.\text{ }\dfrac{1}{\sqrt{k}-\sqrt{k+1}}=\dfrac{\left(\sqrt{k}+\sqrt{k+1}\right)}{\left(\sqrt{k}+\sqrt{k+1}\right)\left(\sqrt{k}-\sqrt{k+1}\right)}\\ =-\left(\sqrt{k}+\sqrt{k+1}\right)\\ \Rightarrow\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}-...-\dfrac{1}{\sqrt{8}-\sqrt{9}}\\ =-\left(\sqrt{1}+\sqrt{2}\right)+\left(\sqrt{2}+\sqrt{3}\right)-\left(\sqrt{3}+\sqrt{4}\right)+...+\left(\sqrt{8}+\sqrt{9}\right)\\ =-\sqrt{1}-\sqrt{2}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+...+\sqrt{8}+\sqrt{9}\\ \\ =\sqrt{9}-\sqrt{1}=2\)
\(2.\text{ }\dfrac{1}{\left(k+1\right)\sqrt{k}+\sqrt{k+1}k}=\dfrac{1}{\sqrt{k\left(k+1\right)}\left(\sqrt{k+1}+\sqrt{k}\right)}\\ =\dfrac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k\left(k+1\right)}\left(\sqrt{k+1}+\sqrt{k}\right)\left(\sqrt{k+1}-\sqrt{k}\right)}\\ =\dfrac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k\left(k+1\right)}\left(k+1-k\right)}=\dfrac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k\left(k+1\right)}}\\ =\dfrac{1}{\sqrt{k}}-\dfrac{1}{\sqrt{k+1}}\\ \Rightarrow\text{ }\dfrac{1}{2\sqrt{1}+1\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+...+\dfrac{1}{7\sqrt{6}+6\sqrt{7}}\\ =\text{ }\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{6}}-\dfrac{1}{\sqrt{7}}\\ =\text{ }\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{7}}\\ \text{ }1-\dfrac{1}{\sqrt{7}}\)
1.\(\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}-\dfrac{1}{\sqrt{4}-\sqrt{5}}+\dfrac{1}{\sqrt{5}-\sqrt{6}}-\dfrac{1}{\sqrt{6}-\sqrt{7}}+\dfrac{1}{\sqrt{7}-\sqrt{8}}-\dfrac{1}{\sqrt{8}-\sqrt{9}}=\dfrac{1+\sqrt{2}}{1-2}-\dfrac{\sqrt{2}+\sqrt{3}}{2-3}+\dfrac{\sqrt{3}+\sqrt{4}}{3-4}-\dfrac{\sqrt{4}+\sqrt{5}}{4-5}+\dfrac{\sqrt{5}+\sqrt{6}}{5-6}-\dfrac{\sqrt{6}+\sqrt{7}}{6-7}+\dfrac{\sqrt{7}+\sqrt{8}}{7-8}-\dfrac{\sqrt{8}+\sqrt{9}}{8-9}=-1-\sqrt{2}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+\sqrt{4}+\sqrt{5}-\sqrt{5}-\sqrt{6}+\sqrt{6}+\sqrt{7}-\sqrt{7}-\sqrt{8}+\sqrt{8}+\sqrt{9}=\sqrt{9}-1=3-1=2\)

b) Ta có: \(\sqrt{\dfrac{3+\sqrt{5}}{3-\sqrt{5}}}+\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}\)
\(=\sqrt{\dfrac{\left(3+\sqrt{5}\right)^2}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}}+\sqrt{\dfrac{\left(3-\sqrt{5}\right)^2}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}}\)
\(=\dfrac{3+\sqrt{5}}{2}+\dfrac{3-\sqrt{5}}{2}\)
\(=\dfrac{3+3}{2}=\dfrac{6}{2}=3\)

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)

1)
a) \(\sqrt{2x-4}\) có nghĩa khi:
\(2x-4\ge0\)
\(\Leftrightarrow2x\ge4\)
\(\Leftrightarrow x\ge\dfrac{4}{2}\)
\(\Leftrightarrow x\ge2\)
b) \(\sqrt{\dfrac{-7}{4-x}}\) có nghĩa khi
\(\dfrac{-7}{4-x}\ge0\) mà \(-7< 0\)
\(\Rightarrow4-x\le0\)
\(\Leftrightarrow x\ge4\)
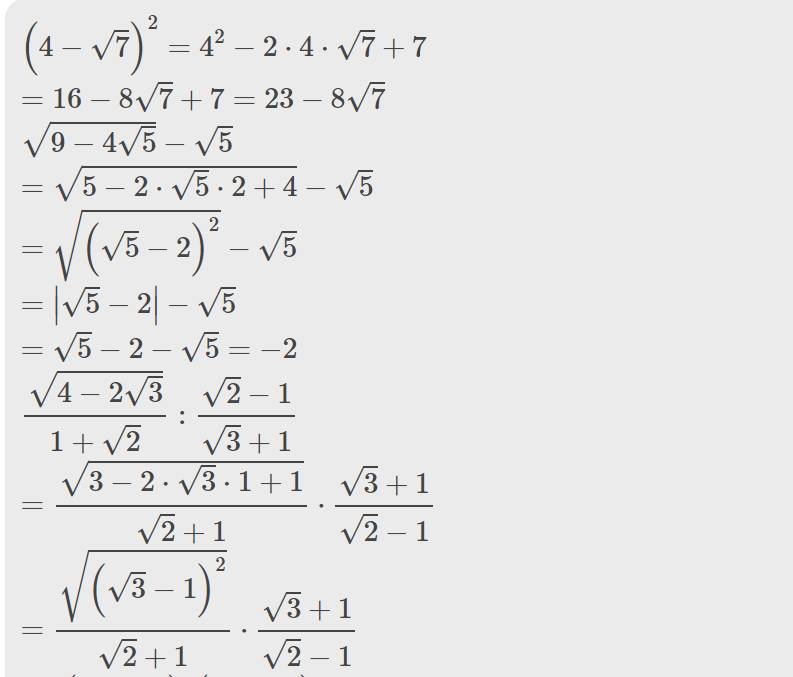
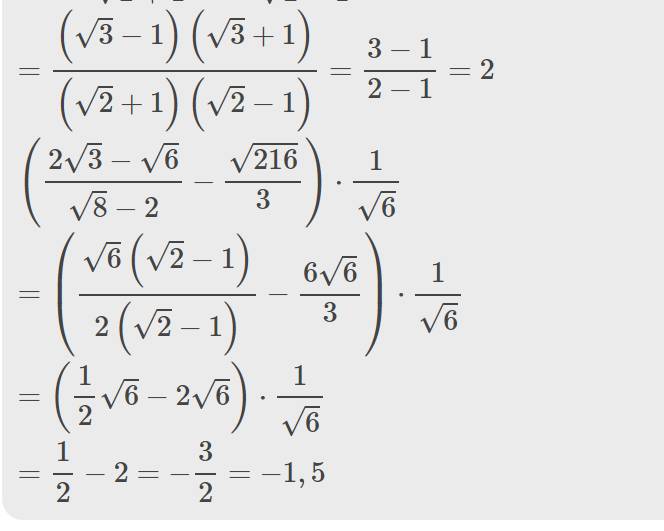
\(\sqrt{\dfrac{9}{7-4\sqrt{3}}}-\sqrt{\dfrac{4}{7+4\sqrt{3}}}\)
\(=\sqrt{\dfrac{9\left(7+4\sqrt{3}\right)}{7^2-\left(4\sqrt{3}\right)^2}}-\sqrt{\dfrac{4\left(7-4\sqrt{3}\right)}{7^2-\left(4\sqrt{3}\right)^2}}\)
\(=\dfrac{3\sqrt{7+4\sqrt{3}}-2\sqrt{7-4\sqrt{3}}}{\sqrt{49-48}}\)
\(=3\sqrt{4+2.2.\sqrt{3}+3}-2\sqrt{4-2.2.\sqrt{3}+3}\)
\(=3\sqrt{\left(2+\sqrt{3}\right)^2}-2\sqrt{\left(2-\sqrt{3}\right)^2}\)
\(=3.\left|2+\sqrt{3}\right|-2.\left|2-\sqrt{3}\right|\)
\(=6+3\sqrt{3}-2+2\sqrt{3}\)
\(=4+5\sqrt{3}\)