(2x+3)2 -2=23
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
25 tháng 5 2022
Số khá xấu. Bạn coi lại đề xem có viết nhầm biểu thức không?
BM
Bài 2: Tìm số tự nhiên x biết:
a) 12(x−1)∶3=43+23 c) (7x−11)3=23.52+200
b) 128−3(x+4)=23 d) 2x+2−2x=96
0
25 tháng 3 2020
Ta có : \(\left(2x+3\right)^2-2=23\)
=> \(\left(2x+3\right)^2=23+2=25\)
=> \(\left[{}\begin{matrix}2x+3=\sqrt{25}\\2x+3=-\sqrt{25}\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=\frac{\sqrt{25}-3}{2}=1\\x=\frac{-\sqrt{25}-3}{2}=-4\end{matrix}\right.\)
Vậy phương trình trên có tập nghiệm là \(S=\left\{1;-4\right\}\)
28 tháng 10 2023
a: \(5^{\left(x-2\right)\left(x+3\right)}=1\)
=>\(\left(x-2\right)\left(x+3\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
c: \(\left|x^2+2x\right|+\left|y^2-9\right|=0\)
mà \(\left\{{}\begin{matrix}\left|x^2+2x\right|>=0\forall x\\\left|y^2-9\right|>=0\forall y\end{matrix}\right.\)
nên \(\left\{{}\begin{matrix}x^2+2x=0\\y^2-9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(x+2\right)=0\\\left(y-3\right)\left(y+3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{0;-2\right\}\\y\in\left\{3;-3\right\}\end{matrix}\right.\)
d: \(2^x+2^{x+1}+2^{x+2}+2^{x+3}=120\)
=>\(2^x\left(1+2+2^2+2^3\right)=120\)
=>\(2^x\cdot15=120\)
=>\(2^x=8\)
=>x=3
e: \(\left(x-7\right)^{x+1}-\left(x-7\right)^{x+11}=0\)
=>\(\left(x-7\right)^{x+11}-\left(x-7\right)^{x+1}=0\)
=>\(\left(x-7\right)^{x+1}\left[\left(x-7\right)^{10}-1\right]=0\)
=>\(\left[{}\begin{matrix}x-7=0\\x-7=1\\x-7=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=8\\x=6\end{matrix}\right.\)
CM
31 tháng 3 2019
a) (2x – 1)(4x2 + 2x + 1) – 4x(2x2 – 3) = 23
⇔ 8x3 – 1 – 8x3 + 12x = 23
⇔ 12x = 24 ⇔ x = 2.
Tập nghiệm của phương trình: S = {2}
b) ĐKXĐ : x + 1 ≠ 0 và x – 2 ≠ 0 (vì vậy x2 – x – 2 = (x + 1)(x – 2) ≠ 0)
⇔ x ≠ -1 và x ≠ 2
Quy đồng mẫu thức hai vế :
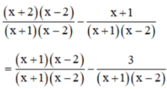
Khử mẫu, ta được : x2 – 4 – x – 1 = x2 – x – 2 – 3 ⇔ 0x = 0
Phương trình này luôn nghiệm đúng với mọi x ≠ -1 và x ≠ 2.
`(2x+3)^2 - 2=23`
`(2x+3)^2 = 23+2`
`(2x+3)^2=25`
`(2x+1)^2=(5)^2`
`@TH1:`
`2x+1=5`
`2x=5-1`
`2x=4`
`x=4:2`
`x=2`
`@TH2:`
`2x+3=-5`
`2x=-5-3`
`2x=-8`
`x=-8;2`
`x=-4`
Vậy `x={-4;2}`