\(\left(x+3\right)^2=144
\)
Các bn giúp mk xem bài này 1 đáp án hay 2 đáp án vs mk cần gấp lắm tks các bn trc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4}{x-2\sqrt{x}}\right)\cdot\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{4}{x-4}\right)\)
<=> \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4}{\sqrt{x}\left(\sqrt{x}-2\right)}\right)\cdot\dfrac{\sqrt{x}-2+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
<=> \(P=\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
<=> \(P=\dfrac{\sqrt{x}+2}{x-2\sqrt{x}}\)
b. Khi \(x=7+4\sqrt{3}=\left(2+\sqrt{3}\right)^2\) => \(\sqrt{x}=2+\sqrt{3}\)
=> \(P=\dfrac{2+\sqrt{3}+2}{7+4\sqrt{3}-2\left(2+\sqrt{3}\right)}=\dfrac{4+\sqrt{3}}{7+4\sqrt{3}-4-2\sqrt{3}}=\dfrac{4+\sqrt{3}}{3+2\sqrt{3}}=\dfrac{5\sqrt{3}-6}{3}\)
check giùm mik

Tổng hai số nguyên tố là một số nguyên tố. Vậy hiệu của 2 số nguyên tố đó là 1 số nguyên tố hay là 1 hợp số .
VD : 7-3 = 4 ( hợp số )
5-2 = 3 ( số nguyên tố )
Chúc bn hok tốt !

\(a)P=\left(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\right).\left(\dfrac{x^2}{x+1}+1\right).\left(x\ne1;x\ne-1\right).\\ P=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}.\dfrac{x^2+x+1}{x+1}.\\ P=\dfrac{x^2-x}{x-1}.\dfrac{1}{x+1}.\\ P=\dfrac{x\left(x-1\right)}{x-1}.\dfrac{1}{x+1}.\\ P=x.\dfrac{1}{x+1}.\\ P=\dfrac{x}{x+1}.\)
\(P=\dfrac{1}{4}.\Rightarrow\dfrac{x}{x+1}=\dfrac{1}{4}.\\ \Leftrightarrow4x-x-1=0.\\ \Leftrightarrow3x-1=0.\\ \Leftrightarrow x=\dfrac{1}{3}\left(TM\right).\)

Hình bạn tự vẽ nha
Gọi G là điểm giao nhau giữa BD và CE
Xét tam giác BGC có: BG + GC >BC
Vì BD và CE là 2 đường trung tuyến của tam giác ABC
=> BG = 2/3 BD ; GC = 2/3 CE
Mà BG + GC = BC
=> 2/3 BD + 2/3 CE > BC
<=>. 2/3 * (BD+CE) > BC
<=> BD + CE > 3/2 BC (ĐPCM)
Vậy BD + CE > 3/2 BC
Dấu * là nhân nha bạn


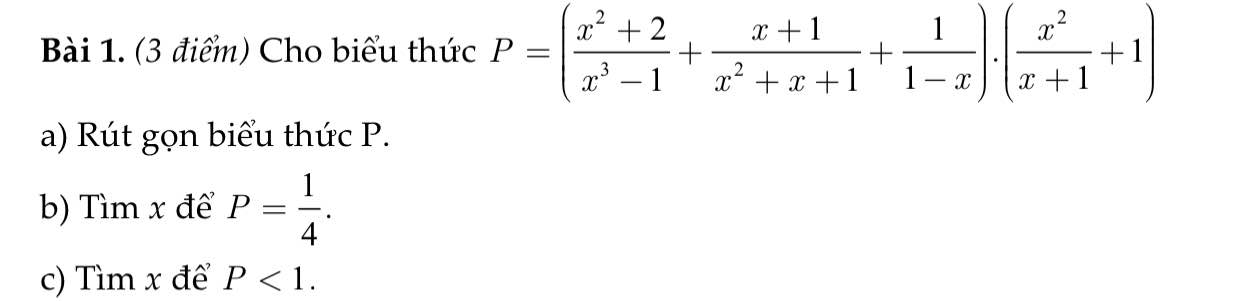
(x+3)^2=144
Thay 144 = 12^2 ta được:
(x+3)^2=12^2
Suy ra: x+3 =12
x =12-3=9
Vậy x =9
K mik nha, thank nhiều nhiều
Theo bài ra ta có \(\left(x+3\right)^2=144\Leftrightarrow\orbr{\begin{cases}x+3=12\\x+3=-12\end{cases}\Leftrightarrow\orbr{\begin{cases}x=9\\x=-15\end{cases}}}\)
Vậy phương trình có 2 đáp án , nếu đề bài hỏi thêm x>0 hay x<0 thì có 1 đáp án thôi nhé :D
__cho_mình_nha_chúc_bạn_học _giỏi__