Câu 2: Từ tỉ lệ thức 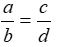(a, b, c, d # 0) ta có thể suy ra:
(giải thích giúp e vs ah , e tks trc nha )
#Toán lớp...
Đọc tiếp
Câu 2: Từ tỉ lệ thức 
(a, b, c, d # 0) ta có thể suy ra:
(giải thích giúp e vs ah , e tks trc nha )
#Toán lớp 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HT
3
Những câu hỏi liên quan
8 tháng 11 2015
ta có :a/b=c/d
=>a/b+1=c/d+1
=>a/b+b/b=c/d+d/d
=>a+b/b=c+d/d
=>dpcm
ta có :a/b=c/d
=>a/b-1=c/d-1
=>a/b-b/b=c/d-d/d
=>a-b/b=c-d/d
=>dpcm
tick cho mik nha bạn !
22 tháng 11 2018
Câu 1
Ta có : \(\frac{a}{b}=\frac{c}{d}=>\left(\frac{a}{b}+1\right)=\left(\frac{c}{d}+1\right)\left(=\right)\frac{a+b}{b}=\frac{c+d}{d}\)
=> ĐPCM
Câu 2
Ta có \(\frac{a}{b}=\frac{c}{d}=>\frac{b}{a}=\frac{d}{c}=>\left(\frac{b}{a}+1\right)=\left(\frac{d}{c}+1\right)\left(=\right)\frac{b+a}{a}=\frac{d+c}{c}=>\frac{a}{b+a}=\frac{c}{d+c}\)
=> ĐPCM
Câu 3
22 tháng 11 2018
Câu 3
Ta có \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)(=) (a+b).(c-d)=(a-b).(c+d)(=)ac-ad+bc-bd=ac+ad-bc-bd(=)-ad+bc=ad-bc(=) bc+bc=ad+ad(=)2bc=2ad(=)bc=ad=> \(\frac{a}{b}=\frac{c}{d}\)
=> ĐPCM
Câu 4
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(=>\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)
Ta có \(\frac{ac}{bd}=\frac{bk.dk}{bd}=k^2\left(1\right)\)
Lại có \(\frac{a^2+c^2}{b^2+d^2}=\frac{b^2k^2+c^2k^2}{b^2+d^2}=\frac{k^2.\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)
Từ (1) và (2) => ĐPCM
9 tháng 12 2023
Câu 1: D
Câu 2: C
Câu 3:
\(\sqrt{\dfrac{9}{49}}=\sqrt{\left(\dfrac{3}{7}\right)^2}=\dfrac{3}{7}\) là số hữu tỉ
\(\sqrt{49}=7\) là số hữu tỉ
\(\sqrt{0,9}=\sqrt{\dfrac{9}{10}}=\dfrac{3}{\sqrt{10}}\) là số vô tỉ
\(\sqrt{0,03}\) là số vô tỉ
=>Trong các số này có hai số là số vô tỉ đó là \(\sqrt{0,9};\sqrt{0,03}\)
VM
0
CT
1
18 tháng 9 2016
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2-b^2}{c^2-d^2}\)mà\(\frac{a^2}{c^2}=\frac{a}{c}.\frac{a}{c}=\frac{a}{c}.\frac{b}{d}=\frac{ab}{cd}\Rightarrow\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\)
V
0
25 tháng 9 2016
ban coi trong sach giao khoa ti le thuc se co mot phan chung minh cho ban thay bang cach dat a/b=c/d=k nha
NN
2
LM
15 tháng 6 2017
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Đặt \(\frac{a}{c}=\frac{b}{d}=k\)
\(\Rightarrow\left(\frac{a}{c}\right)^2=k^2;\frac{a}{c}.\frac{b}{d}=k^2\Rightarrow\frac{a^2}{c^2}=\frac{ab}{c\text{d}}\left(=k^2\right)\)
(Bạn xem cách trình bày có hợp lý không giúp mình nha!)
ai giúp e đuyyyyyy ạ ?:((((