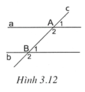
cho hình vẽ bên, biết rằng: A1+B1=A2+B2 chứng tỏ rằng a // b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tìm cách giải
Trong hình vẽ đã có những cặp góc đồng vị, cặp góc trong cùng phía. Từ điều kiện trong đề bài, ta có thể suy ra được tổng của hai góc trong cùng phía bù nhau, từ đó suy ra được hai đường thẳng song song.
Trình bày lời giải
Ta có A 2 ^ − A 1 ^ = B 2 ^ − B 1 ^ , suy ra A 2 ^ + B 1 ^ = B 2 ^ + A 1 ^ .
Mặt khác A 2 ^ + B 1 ^ + B 2 ^ + A 1 ^ = 360 ° nên A 2 ^ + B 1 ^ = 180 ° .
Suy ra a // b vì có cặp góc trong cùng phía bù nhau

Tham khảo : Câu hỏi của huy nguyễn - Toán lớp 7 - Học toán với OnlineMath

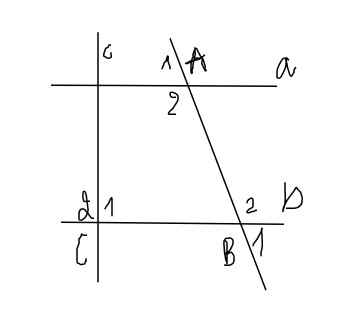
Ta có A 1 ^ + A 2 ^ + B 2 ^ = a ° ⇒ B 2 ^ = a ° − 180 ° (1)
B 1 ^ + B 2 ^ + A 1 ^ = b ° ⇒ A 1 ^ = b ° − 180 ° (2)
Từ (1) và (2), suy ra: B 2 ^ + A 1 ^ = a ° + b ° − 360 ° = 540 ° − 360 ° = 180 ° .
Mặt khác A 2 ^ + A 1 ^ = 180 ° (kề bù) nên B 2 ^ + A 1 ^ = A 2 ^ + A 1 ^ = 180 ° .
Suy ra B 2 ^ = A 2 ^ . Do đó a // b vì có cặp góc đồng vị bằng nhau

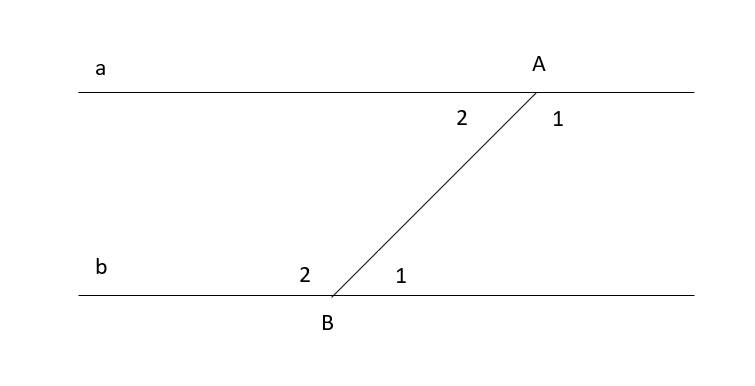
Ta có: a//b nên \(\widehat{A_2}+\widehat{B_2}=180^0\)(2 góc kề bù)
Mà \(\widehat{A_2}-\widehat{B_2}=30^0\left(gt\right)\)
\(\Rightarrow\widehat{A_2}=\left(180^0+30^0\right):2=105^0\)
Ta có: a//b(gt)
\(\Rightarrow\widehat{A_2}=\widehat{B_1}=105^0\)( 2 góc so le trong)
Ta có: \(\widehat{A_2}+\widehat{A_1}=180^0\)(2 góc kề bù)
\(\Rightarrow\widehat{A_1}=180^0-\widehat{A_2}=180^0-105^0=75^0\)

\(a)\) m U n 2 1 1 2 36 o 36 o p V q
b) U1 + V1= 180o (kề bù)
V1= 180o -U1 = 180o - 36o= 144o
U2 = V1 (đồng vị)
=> U2= 144o
Vậy V1= U2= 144o