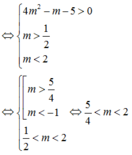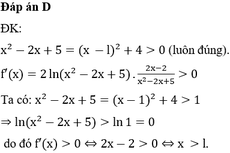Cho hàm số f(x) = x2 -1 . Tìm các giá trị của x sao cho f(1-x) nhận giá trị âm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Thay x=-2 vào hàm số \(f\left(x\right)=2x^2-5\),ta được:
\(f\left(-2\right)=2\cdot\left(-2\right)^2-5=2\cdot4-5=8-5=3\)
Thay x=1 vào hàm số \(f\left(x\right)=2x^2-5\), ta được:
\(f\left(1\right)=2\cdot1^2-5=2-5=-3\)
Thay x=3 vào hàm số \(f\left(x\right)=2x^2-5\), ta được:
\(f\left(3\right)=2\cdot3^2-5=2\cdot9-5=18-5=13\)
Vậy: f(-2)=3
f(1)=-3
f(3)=13
b) Để f(x)=3 thì \(2x^2-5=3\)
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=3 thì \(x\in\left\{2;-2\right\}\)

Ta có: \(f\left(x\right)=x^2-1\)
\(\Rightarrow f\left(1-x_0\right)=\left(1-x_0\right)^2-1\)
\(=x_0^2-2x_0+1-1=x_0^2-2x_0\)
\(=x_0\left(x_0-2\right)\)
\(f\left(1-x_0\right)< 0\Leftrightarrow\)\(x_0\left(x_0-2\right)< 0\)
Mà \(x_0>x_0-2\)nên \(\hept{\begin{cases}x_0>0\\x_0-2< 0\end{cases}}\Leftrightarrow0< x_0< 2\)
Vậy \(0< x_0< 2\)thì \(f\left(1-x_0\right)\)đạt giá trị âm

a) Để y nhận giá trị âm điều kiện là : 3x - 1 < 0 ↔ 3x < 1 ↔ x < \(\frac{1}{3}\)
Vậy với x < \(\frac{1}{3}\) thì y nhận giá trị âm
b) Để y nhận giá trị lớn hơn 5 điều kiện là : 3x - 1 > 5 ↔ 3x > 6 ↔ x > 2
Vậy với x > 2 thì y nhận giá trị lớn hơn 5

Đáp án D
- Phương pháp: Sử dụng công thức 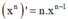 và
và 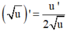 tính f'(x). Từ đó giải bất phương trình.
tính f'(x). Từ đó giải bất phương trình.
- Cách giải:
+ Ta có: 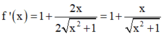
+ Theo đề bài ta có: 2x.f'(x) - f(x) ≥ 0.
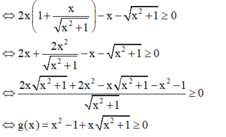
+ Thử các đáp án:
+ Với 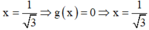 thuộc tập nghiệm của BPT.
thuộc tập nghiệm của BPT.
⇒ Loại đáp án A, B và C.