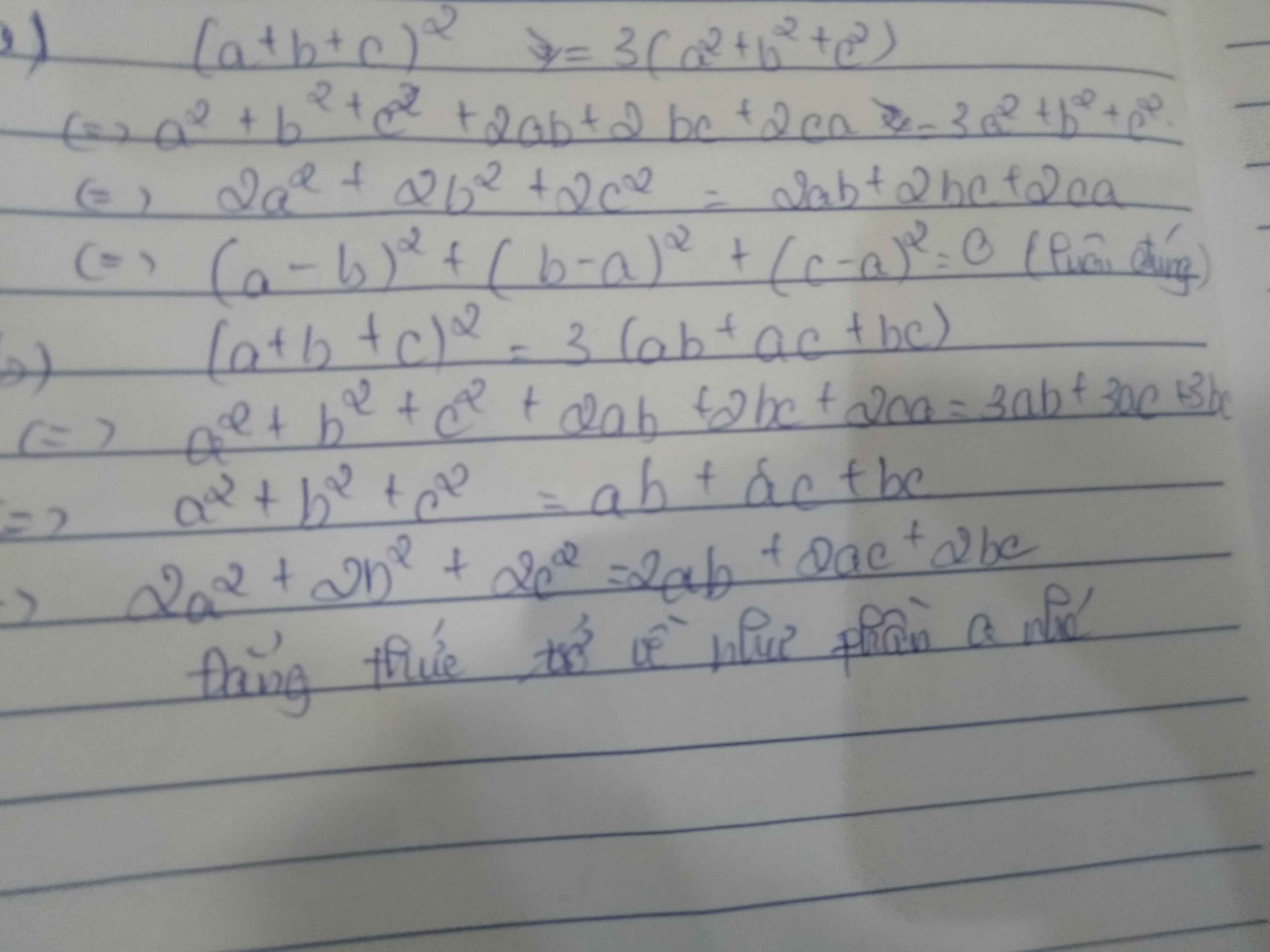cmr : a2+b2+c2 ≧ 2(ab+bc-ac)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(\left(a+b+c\right)^2=a^2+b^2+c^2\Leftrightarrow ab+bc+ca=0\)
\(\Rightarrow a^3b^3+b^3c^3+c^3a^3=3a^2b^2c^2\)
Ta có:
\(\dfrac{bc}{a^2}+\dfrac{ac}{b^2}+\dfrac{ab}{c^2}=\dfrac{a^3b^3+b^3c^3+c^3a^3}{a^2b^2c^2}=\dfrac{3a^2b^2c^2}{a^2b^2c^2}=3\)
TA
0
HT
0
HT
0
14 tháng 7 2021
`1)(a+b+c)^2=3(a^2+b^2+c^2)`
`<=>a^2+b^2+c^2+2ab+2bc+2ca=3a^2+3b^2+3c^2`
`<=>2ab+2bc+2ca=2a^2+2b^2+2c^2`
`<=>a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=0`
`<=>(a-b)^2+(b-c)^2+(c-a)^2=0`
Mà `(a-b)^2+(b-c)^2+(c-a)^2>=0`
Vậy dấu "=" xảy ra chỉ có thể là `a=b=c`
`2)(a+b+c)^2=3(ab+bc+ca)`
`<=>a^2+b^2+c^2+2ab+2bc+2ca=3ab+3bc+3ca`
`<=>a^2+b^2+c^2=ab+bc+ca`
`<=>2ab+2bc+2ca=2a^2+2b^2+2c^2`
`<=>a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2=0`
`<=>(a-b)^2+(b-c)^2+(c-a)^2=0`
Mà `(a-b)^2+(b-c)^2+(c-a)^2>=0`
Vậy dấu "=" xảy ra chỉ có thể là `a=b=c`
Vậy nếu `a=b=c` thì ....
