1, Cho hình thang cân ABCD (AB //, AB < CD). Gọi M, N, P, Q lần lượt là trung điểm các đoạn thẳng AD, BD, AC, BC .a, Chứng minh 4 điểm M, N, P, Q thẳng hàng .b, Chứng minh tứ giác ABPN là hình thang cân.c, Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật2, Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB .a,...
Đọc tiếp
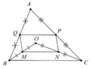
1, Cho hình thang cân ABCD (AB //, AB < CD). Gọi M, N, P, Q lần lượt là trung điểm các đoạn thẳng AD, BD, AC, BC .
a, Chứng minh 4 điểm M, N, P, Q thẳng hàng .
b, Chứng minh tứ giác ABPN là hình thang cân.
c, Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật
2, Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB .
a, Chứng minh tứ giác MNPQ là hình bình hành.
b, Xác định vị trí của điểm O Để tứ giác MNPQ là hình chữ nhật
3, Cho tam giác ABC Vuông cân tại C. Trên các cạnh AC , BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm B vẽ PM // BC ( M thuộc AB) Chứng minh tứ giác PCQM là hình chữ nhật
M.N VẼ HÌNH GIÚP LUÔN NHÉ. THANKS NHIỀU Ạ

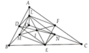
a, Xet tam giac CDE co :
KC=KD va CI=IE
=> KI la tdb
=> KI=1/2DE va KI//DE (1)
Xet tam giac
Xét tam giác DOE co :
DM=MO va ON=NE
=>MN la tdb
=> MN=1/2 DE va MN//DE (2)
Từ(1)(2) suy ra : MNIK la HBH
b, Xét tam giác CDO co :
KC=KD
DM=MO
=> KM là dtb tam giác CDO
=> KM=1/2 OC
Va KM//OC
=> KM vuông góc với MN =>M=90
Mà trong hình bình hành có một góc vuông là hình chữ nhật
Vậy O là phải thỏa mãn diện kiến là trực tâm (giao điểm của 3 đường cao) đệ tứ giác MNIK là hình chữ nhật .