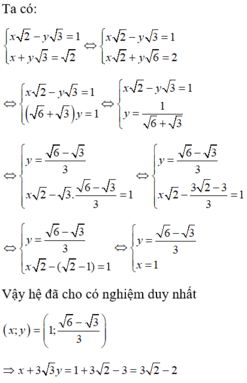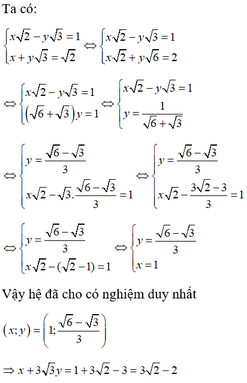Tìm các nghiệm nguyên (x,y) của phương trình: 54x3+1=y3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+, Nếu x = 0 => ko tồn tại y thuộc Z
+, Nếu x khác 0 => x^2 >= 1 => x^2-1 >= 0
Có : y^3 = x^3+2x^2+3x+2 > x^3 ( vì 2x^2+3x+2 > 0 )
Lại có : y^3 = (x^3+3x^3+3x+1)-(x^2-1) = (x+1)^3 - (x^2-1) < = (x+1)^3
=> x^3 < y^3 < = (x+1)^3
=> y^3 = (x+1)^3
=> x^2-1 = 0
=> x=-1 hoặc x=1
+, Với x=-1 thì y = 0
+, Với x=1 thì y = 2
Vậy .............
Tk mk nha
Ta có: \(x^3+2x^2+3x+2=y^3\) (1)
Xét \(2x^2+3x+2=2\left(x^2+\frac{3}{2}x\right)+2=2\left(x^2+\frac{3}{2}x+\frac{9}{16}\right)+2-2.\frac{9}{16}\)
\(=2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\) Vì \(\left(x+\frac{3}{4}\right)^2\ge0\Rightarrow2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\ge\frac{7}{8}>0\)
\(\Rightarrow y^3>x^3\Rightarrow y^3\ge\left(x+1\right)^3\)
\(\Rightarrow x^3+2x^2+3x+2\ge\left(x+1\right)^3\) \(\Rightarrow x^3+2x^2+3x+2\ge x^3+3x^2+3x+1\)
\(\Rightarrow x^3+3x^2+3x+1-x^3-2x^2-3x-2\le0\)
\(\Rightarrow x^2-1\le0\Rightarrow x^2\le1\) Vì \(x\in Z\Rightarrow\orbr{\begin{cases}x^2=1\\x^2=0\end{cases}}\)
+ TH1: x2 = 0 => x =0 Thay vào pt (1) ta được y3 = 2 (loại) vì y nguyên
+ TH2 : x2 = 1 => \(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Thay x=1 vào pt (1) ta đc: 1+2+3+2 = 8 = y3 => y = 2
Thay x= -1 vào pt (1) ta đc: -1 + 2 -3 +2 = 0 =y3 => y = 0
Vậy cặp (x;y) là (1;2) ; (-1;0).

Ta có: x 3 + y 3 = ( x + y ) 2 < = > ( x + y ) ( x 2 − x y + y 2 − x − y ) = 0
Vì x, y nguyên dương nên x+y > 0, ta có: x 2 − x y + y 2 − x − y = 0
⇔ 2 ( x 2 − x y + y 2 − x − y ) = 0 ⇔ x - y 2 + x - 1 2 + ( y - 1 ) 2 = 2
Vì x, y nguyên nên có 3 trường hợp:
+ Trường hợp 1: x − y = 0 x - 1 2 = 1 ⇔ x = y = 2 , z = 4 y - 1 2 = 1
+ Trường hợp 2: x − 1 = 0 x - y 2 = 1 ⇔ x = 1 , y = 2 , z = 3 y - 1 2 = 1
+ Trường hợp 3: y − 1 = 0 x - y 2 = 1 x - 1 2 = 1 ⇔ x = 2 , y = 1 , z = 3
Vậy hệ có 3 nghiệm (1,2,3);(2,1,3);(2,2,4)

Ta có
x 2 − y 3 = 1 x + y 3 = 2 ⇔ x 2 − y 3 = 1 x 2 + y 6 = 2 ⇔ x 2 − y 3 = 1 6 + 3 y = 1 ⇔ x 2 − y 3 = 1 y = 1 6 + 3 ⇔ y = 6 − 3 3 x 2 − 3 . 6 − 3 3 = 1 ⇔ y = 6 − 3 3 x = 1
Vậy hệ đã cho có nghiệm duy nhất ( x ; y ) = 1 ; 6 − 3 3
Đáp án: D

Tui vừa trả lời 3 bài này ở câu của Nguyễn Anh Quân
Xem tui giải đúng không nha
Xin  Wrecking Ball nhận xét
Wrecking Ball nhận xét

các bạn ơi giải bài này đi mình cần gấp ai giả được minh cho 1 thích nhé

\(\left\{{}\begin{matrix}mx+y=2m\\x+my=m+1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=2m-mx\\x+m\left(2m-mx\right)=m+1\left(1\right)\end{matrix}\right.\)
(1) ⇔x+2m2-m2x=m+1
⇔x(1-m2)=m+1-2m2
TH1: 1-m2=0
⇔m=\(\pm\)1
-Thay m= 1 vào (2) ta có: 0x =0 (luôn đúng)
⇒m=1(chọn)
-Thay m=-1 và (2) ta có: 0x=-2 (vô lí)
⇒m=-1(loại)
TH2: 1-m2 ≠ 0
⇔m ≠ \(\pm\) 1
⇒HPT có nghiệm duy nhất:
x= \(\dfrac{-2m^2+m+1}{1-m^2}\)
y= \(2m-m.\dfrac{-2m^2+m+1}{1-m^2}\)
⇔y= \(2m+\dfrac{-2m^3-m^2-m}{1-m^2}\)