cho tam giác ABC vuông cân tại A.Vẽ ra phía ngoài tam giác đều ABM và ACN.
a)tính góc MBC
b)kẻ AI vuông góc với BC chứng minh MI =NI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
10 tháng 12 2016
ta có
góc MBA=60 ( tam giác BMA đều)
góc ABC =45 ( tam giác ABC vuông cân tại A)
-> góc MBA+góc ABC =60+45
-> góc MBC=105
b)Xét tam giác ABC vuong cân tại A ta có
AI là duong cao ( AI vuông góc BC)
-> AI là phân giác
-> góc BAI = góc IAC
ta có
góc MAB= góc NAC (=60)
góc BAI= góc IAC (cmt)
-> góc MAB+ góc BAI = góc NAC + góc IAC
-> góc MAI = góc IAN
ta có
AM=AB (( tam giác MBA deu)
AB=AC ( tam giác ABC vuông cân tại A)
AC= AN ( tam giác ANC đều)
=> AM=AN
Xét tam giác MAI và tam giác NAI ta có
AM=AN (cmt)
AI=AI (cc)
góc MAI= góc NAI (cmt)
-> tam giác MAI = tam giác NAI (cgc)
-> MI = NI
NH
29 tháng 2 2020
a, Vì △ABC vuông cân tại A => AB = AC (1) và ^ABC = ^ACB = 45o
Vì △ABM đều => AB = AM = BM (2) và ^ABM = ^BAM = ^BMA = 60o
Vì △ACN đều => AC = CN = AN (3) và ^ACN = ^CAN = ^CNA = 60o
Ta có: ^MBC = ^MBA + ^ABC = 60o + 45o = 105o
b, Xét △AIC vuông tại I và △AIB vuông tại I
Có: AC = AB (cmt)
AI là cạnh chung
=> △AIC = △AIB (ch-cgv)
=> IC = IB (2 cạnh tương ứng)
=> AI là trung tuyến của △ABC vuông cân tại A
=> IA = IC = IB = (1/2) . BC
c, Từ (1) ; (2) ; (3) => BM = CN
Ta có: ^NCI = ^NCA + ^ACI = 60o + 45o = 105o
Xét △NCI và △MBI
Có: NC = MB (cmt)
NCI = MBI (= 105o)
IC = IB (cmt)
=> △NCI = △MBI (c.g.c)
=> IN = IM (2 cạnh tương ứng)
2 tháng 3 2023
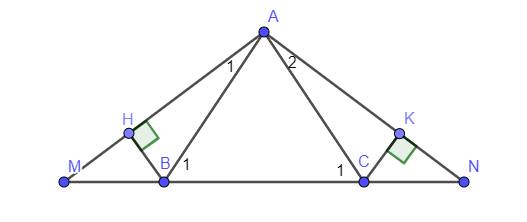
`a)`
Có `Delta ABC` cân tại `A=>hat(B_1)=hat(C_1);AB=AC`
Có `hat(B_1)+hat(ABM)=180^0` ( kề bù )
`hat(C_1)+hat(ACN)=180^0` (kề bù)
mà `hat(B_1)=hat(C_1)(cmt)`
nên `hat(ABM)=hat(ACN)`
Xét `Delta ABM` và `Delta ACN` có :
`AB=C(cmt)`
`hat(ABM)=hat(ACN)(cmt)`
`BM=CN(GT)`
`=>Delta ABM=Delta ACN(c.g.c)(đpcm)`
`b)`
Có `Delta ABM=Delta ACN(cmt)=>hat(A_1)=hat(A_2)` ( 2 góc t/ứng )
Xét `Delta AHB` và `Delta AKC` có :
`hat(AHB)=hat(AHC)(=90^0)`
`AB=AC(cmt)`
`hat(A_1)=hat(A_2)(cmt)`
`=>Delta AHB=Delta AKC(c.h-g.n)(đpcm)`
12 tháng 5 2023
a: Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
=>ΔABM=ΔACM
b: Xét ΔAIM vuông tạiI và ΔAKM vuông tại K có
AM chung
góc IAM=góc KAM
=>ΔAIM=ΔAKM
=>AI=AI và MI=MK
c:AI=AK
MI=MK
=>AM là trung trực của IK=>AM vuông góc IK