Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
(*) Vì AM = AN nên ΔAMN cân tại A
=> góc AMN = ANM ( 2 góc đáy)
mà AMN + ANM = 180 - BAC => AMN = (180 - BAC) :2 (1)
Do ΔABC cân tại A nên góc ABC = ACB hay MBC = NCB
mà góc ABC + ACB = 180 - BAC => ABC = (180 - BAC ) : 2 (2)
Từ (1) và (2) suy ra AMN = ABC
do 2 góc này ở vị trí so le trong nên MN // BC → đpcm
(*) Ta có: AM + MB = AB
AN + NC = AC
mà AM = AN; AB = AC => MB = NC
Xét ΔBMC và ΔCNB có:
BM = CN (cm trên)
góc MBC = NCB (cm trên)
BC chung
=> ΔBMC = ΔCNB (c.g.c)
=> MC = NB (2 cạnh tương ứng) → đpcm
Vì AM = AN (gt) nên t/g AMN cân tại A
=> AMN = ANM
=> MAN = 180o - 2.AMN
Vì t/g ABC cân tại A nên ABC = ACB
=> BAC = 180o - 2.ABC (2)
Từ (1) và (2) => AMN = ABC
Mà AMN và ABC là 2 góc ở vị trí đồng vị nên MN // BC (1)
Xét t/g ABN và t/g ACM có:
AB = AC (gt)
A là góc chung
AN = AM (gt)
Do đó, t/g ABN = t/g ACM (c.g.c)
=> BN = CM (2 cạnh tương ứng) (2)
(1) và (2) là đpcm
Vì tam giác ABC cân tại A nên \(\widehat{A}=\widehat{B}\)
\(\Rightarrow\widehat{B}=\frac{180^o-\widehat{A}}{2}\)
= \(\frac{180^o-100^o}{2}=40^o\) ( 1 )
Mà AM = AN ( gt ) nên \(\Delta AMN\) cân tại A \(\Rightarrow\widehat{AMN}=\widehat{ANM}\)
\(\Rightarrow\widehat{AMN}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-100^o}{2}=40^o\) ( 2)
Từ ( 1 ) và ( 2 ) \(\Rightarrow\widehat{B}=\widehat{AMN}\)
Vậy \(MN//BC\) ( vì có cặp góc ở vị trí đồng vị bằng nhau )
Chúc bạn học tốt !!!
Bạn tự vẽ hình nha!
do AN=AM=>Tam giác AMN cân
do tam giác ABC cân \(\Rightarrow\widehat{B}=\widehat{C}=\frac{180-\widehat{A}}{2}=\frac{180-100}{2}=40\)
và tam giác AMN cân \(\Rightarrow\widehat{M}=\widehat{N}=\frac{180-\widehat{A}}{2}=\frac{180-100}{2}=40\)
do \(\widehat{M}=\widehat{B}\)
do hai góc đồng vị =>MN//BC
do tam giác abc cân tại a
=>góc abc=180-2*góc a
do am=an
=>tam giác amn can taị a
=>góc amn=180-2*góc a
=>góc amn=góc abc(vì cùng bằng
180-2*góc a)
mà hai góc này ở vị trí so le trong
=>mn song song vs ab
xét 2 tam giác abn và acm có
chung góc a
am=an
ab=ac
=>tg abn=tg acm
=>bm=cm(2 cạnh tương ứng)
cau 2
theo đề bài ta có
tg abc đều =>ab=bc=ca
ad=be=cf
=>ab-ad=bc-be=ac-cf
hay bd=ce=af
xét 3 tg ade,bed và cef ta có
góc a=gócb=gócc
ad=be=cf
bd=ce=af
=> tg ade= tg bed= tg cef
=>de=df=ef
=>tg def là tg đều
tam giac ABC can tai A=>goc B=180-100/2=40(1)
ta co AN+NC=AC
AM+MB=AB
ma AM=AN,AB=AC
=>NC=BM=>tam giac AMN can tai A
tam giac AMN can tai A=>goc M=180-100/2=40(2)
tu (1)(2)=.B=M ma hai goc nay o vi tri dong vi =>MNsog sog BC (tick nha)
Vì \(\Delta ABC\)là tam giác cân tại A
=> \(\widehat{B}=\widehat{C}\)( hai góc ở đáy )
=> \(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{80^0}{2}=40^0\)
Xét \(\Delta AMN\)có \(AM=AN\)
=> \(\Delta AMN\)là tam giác cân tại A
=> \(\widehat{M}_1=\widehat{N}\)( hai góc ở đáy )
Lại có : \(\widehat{M_1}+\widehat{N}=180^0-\widehat{A}=180^0-100^0=80^0\)
=> \(\widehat{M_1}=\widehat{N}=\frac{80^0}{2}=40^0\)
Ta có : \(\widehat{M_1}+\widehat{M_2}=180^0\)( kề bù )
=> \(\widehat{M_2}=180^0-\widehat{M_1}=180^0-40^0=140^0\)
Ta có : \(\widehat{B}+\widehat{M_2}=40^0+140^0=180^0\)( 1 )
mà \(\widehat{B}\)và \(\widehat{M_2}\)ở vị trí trong cùng phía ( 2 )
Từ ( 1 ) và ( 2 ) => \(MN//BC\)( đpcm )
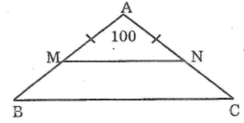
a) +Xét tam giác ABC cân tại A có \(\widehat{A}\)= 100o
=>\(\widehat{B}=\widehat{C}=40^o\)
TT ta có: Tam giác AMN cân(AM=AN) tại A có\(\widehat{A}\)=100o
=>\(\widehat{AMN}=\widehat{ANM}=40^o\)
=>\(\widehat{B}=\widehat{C}\)\(=\widehat{AMN}=\widehat{ANM}\)
=>\(\widehat{B}=\widehat{AMN}\)
Mà hai góc này đồng vị =>MN//BC
+Xét tam giác AMC và tam giác ANB có:
AM=AN
 chung
AC=AB
Do đó tam giác AMC= tam giác ANB(c.g.c)
Suy ra BN=CM(hai cạnh t.ứ)
Bài 2 để tí mik lm tiếp, mik đag bận, bạn tích mik để mik có cái để tl tiếp nhé
Chúc học tốt