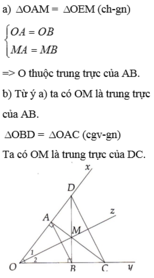
bài 1 Cho góc xoy có oz là tia phân giác ,M là điểm bất kỳ thuộc tia oz .Qua M kể đường thẳng a vuông góc với ox tại A cắt oy tại C và vẽ đường thẳng b vuông góc với oy tại B cắt tia ox tại D a...

QT

Quynh Truong

18 tháng 4 2021

bài 1 Cho góc xoy có oz là tia phân giác ,M là điểm bất kỳ thuộc tia oz .Qua M kể đường thẳng a vuông góc với ox tại A cắt oy tại C và vẽ đường thẳng b vuông góc với oy tại B cắt tia ox tại D a) Chứng minh tam giác AMO bằng tam giác BOM từ đó suy ra OM là đường trung trực của đoạn thẳng AB b) Tam giác DMC là tam giác gì ? Vì sao? c)Chứng minh...

Đọc tiếp

#Toán lớp 7

0

PT

Pham Trong Bach

20 tháng 4 2018

Cho góc xOy khác góc bẹt Oz là tia phân giác của góc xOy. Gọi M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:a) Điểm O thuộc đường trung trực của AB;b) OM là đường trung trực của AB; Điểm M thuộc đường trung trực của...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

20 tháng 4 2018

Đúng(0)

DT

Doãn Trịnh Việt Thảo

9 tháng 5 2018 - olm

cho góc xOy nhọn , Oz là tia phân giác của góc xOy. M là 1 điểm thuộc tia Oz (M không trùng với O). qua, vẽ đường thẳng a vuông góc với Ox tại A, cắt

Oy tại C. vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh OM vuông góc với CD

#Toán lớp 7

0

HN

Hứa Nhật Minh

24 tháng 4 2017 - olm

Cho góc xOy có Oz là tia phân giác , M là điểm bất kỳ thuộc tia Oz. Qua M kẻ đường thẳng a vuông góc với Ox tại A cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D

a) chứng minh tam giác AOM bằng tam giác BOM từ đó suy ra OM là đường trung trực của đoạn thẳng AB

b) tam giác DMC là tam giác gì ? Vì sao ?

c) chứng minh DM + AM < DC

#Toán lớp 7

1

DH

Đào Hà Anh

28 tháng 5 2020

a) Xét ΔAOM và ΔBOM có:

+ Góc AOM = BOM.

+ OM là cạnh huyền chung.

+ Góc OAM = OBM = 90.

Nên ΔAOM = ΔBOM (ch-gn).

=>OM là đường trung trực của đoạn thẳng AB.

b) tam giác DMC là tam giác cân.

Xét ΔADM và ΔBCM có:

+ Góc MAD = MBC = 90.

+ Góc AMD = CMB (đối đỉnh).

+ AM = BM (ΔAOM = ΔBOM).

Nên ΔADM = ΔBCM (g.c.g).

=> DM = CM.

Nên ΔDMC là tam giác cân.

c) Ta có ΔDMC là tam giác cân, Nên DM + MC > DC.

Xét ΔADM có AM là cgv nên: AM< DM =>2AM < DC.

<=> AM + DM < DC

Đúng(1)

BT

Bảo Trân Nguyễn Hoàng

4 tháng 3 2018 - olm

Cho xÔy có Oz là tia phân giác M là điểm bất kỳ thuộc tia OZ. QUa M kẻ đừng thẳng a vuông góc với Õ tại A cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D

a) Chứng minh tam giác AOM bằng tam giác BOM từ đó suy ra OM là đường trung trực của đoạn thẳng AB

b) Tam giác DMC là tam giác gì? Vì sao?

#Toán lớp 7

2

NT

Nguyễn Thanh Vy

11 tháng 3 2018

A/
* Xét T/g AOM và T/g BOM có :
+ O₁= O₂ ( Oz là p/g AOB )
+ OAM = OBM ( = 90⁰ )
+ AM chung
=> t/g AOM = BOM ( ch.gn )
* Xét T/g AMH và T/g BMH có :
+ AM = BM ( T/g AOM= BOM )
+ Góc AMH = BMH ( T/g AOM = BOM )
+ MH chung
=> T/g AMH = T/g BMH (c.g.c)
=> AH = BH
* Xét t/g AOH và T/g BOH có :
+ AH = BH ( cmt )
+ OH chung
+ OA = OB ( T/g AOM = T/g BOM )
=> T/g AOH = T/g BOH (c.c.c)
* Ta có :
+ AH = BH ( cmt ) (1)
+ H₁= H₂ ( T/g AOH = T/g BOH ) (2)
mà H₁ + H₂ = 180^o ( Kb )
- (1) , (2) => H₁ = H₂ = 90^o
=> OM là trung trực của đoạn thẳng AB
B/ Xét T/g AMD và T/g BMC có :
+ AM = BM ( T?g AOM = T/g BOM )
+ Góc DAM = CAM ( = 90^o )
+ M₁ = M₂ ( đđ )
=> T/g AMD = T/g BMC ( ch. gn )
=> MD = MC
=> T/g DMC cân tại D

Đúng(1)

NT

Nguyễn Thanh Vy

11 tháng 3 2018

Đúng(0)

DT

Đinh Thị Thuý Quỳnh

30 tháng 12 2015 - olm

Cho góc nhọn xOy, Oz là tia phân giác của xOy. qua điểm A thuộc tia Ox vẽ đường thẳng song song với Oy cắt Oz tại M. Qua M kẻ đường thẳng song song với Ox cắt Oy tại B.Chứng minh:

a/OA=MB ; MA=OB.

b/ Từ M kẻ MH vuông góc với Ox ; MK vuông góc với Oy. Chứng minh MH=MK

#Toán lớp 7

0

OI

✞ঔৣ۝ŧɦịռɦ ɕυŧε❤⁀ᶦᵈᵒ

6 tháng 11 2021

Cho góc nhọn xoy và oz là tia phân giác của xoy.Qua điểm A thuộc tia õ, vẽ đường thẳng song song với oy cắt oz tại M.Qua M kẻ đường thẳng song song với ox cắt tại oy tại B.

A)Từ M vẽ MH vuông góc Ox(H thuộcOx),Mk vuông góc Oy(K thuộc Oy).Chứng minh MH=Mk.

B)Chứng minh Om vuông góc HK

#Toán lớp 7

0

UT

uyen tran

15 tháng 12 2020

cho oz là tia phân giác của góc nhọn xoy. từ điểm m trên oz (m khác o) kẻ đường thẳng vuông góc với oy cắt oy tại k và cắt ox tại a. cũng từ m kẻ đường thẳng vuông góc với ox cắt ox tại h và cắt oy tại b . a, chứng minh tam giác ohm= tam giác okm b, chứng minh oa=ob

#Toán lớp 7

0

KT

Khánh Tạ Quốc

15 tháng 12 2021

Cho xOy < 90o có Oz là tia phân giác. Từ điểm M trên tia Oz, vẽ một đường thẳng song song với Oy cắt Ox tại A. Từ M vẽ đường thẳng song song Ox, cắt Oy tại B.

a) Chứng minh: OA = OB

b) Vẽ MH vuông góc Ox tại H , MK vuông góc Oy tại K. Chứng minh : MH = MK

c) Chứng minh OM là trung trực của AB

#Toán lớp 7

0