Tìm chữ số thích hợp thay vào dấu * để số 3744* chia hết cho cả 2,3 và 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 7 2015
Bài lúc nãy thiếu, đầy đủ nek:
Chia hết cho cả 2 và 5 thì tận cùng phải là 0
=> *250 => ta được tổng 2+5+0=7
Mà chia hết cho 3 thì tổng các chữ số phải chia hết cho 3
=> Vì ko có điều kiện 2 ta được các số 2250 ; 5250 hoặc 8250
HQ
Hà Quang Minh
Giáo viên
9 tháng 10 2023
a) *\( \in \){0; 2; 4; 6; 8}
b) *\( \in \){0; 5}
c) *\( \in \){0}
6 tháng 10 2017
17** chia het cho 2;3 va chia 5 du 1 => số * tận cùng là 1 số chia hết cho 2 va chia 5 dư 1=>dau * tận cùng là 6
Để 17*6 chia hết cho 3 thì 1+7+*+6 phải chia hết cho 3 hay 14+* chia hết cho 3 => * =1;4;7
Vậy 17**=1716
1746
1776
10 tháng 12 2023
Bài 1:
Đặt \(X=\overline{4a2b}\)
X chia hết cho 2;5 nên X chia hết cho 10
=>X có chữ số tận cùng là 0
=>b=0
=>\(X=\overline{4a20}\)
X chia hết cho 9
=>\(\left(4+a+2+0\right)⋮9\)
=>\(\left(a+6\right)⋮9\)
=>a=3
vậy: X=4320
Bài 2:
Đặt \(A=\overline{20a2b}\)
A chia hết cho 25 mà A có tận cùng là \(\overline{2b}\)
nên b=5
=>\(A=\overline{20a25}\)
A chia hết cho 9
=>\(2+0+a+2+5⋮9\)
=>\(a+9⋮9\)
=>\(a⋮9\)
=>\(a\in\left\{0;9\right\}\)
Bài 3:
Đặt \(B=\overline{3x57y}\)
B chia 5 dư 3 nên B có tận cùng là 3 hoặc 8(1)
B chia 2 dư 1 nên B có tận cùng là số lẻ (2)
Từ (1),(2) suy ra B có tận cùng là 3
=>y=3
=>\(B=\overline{3x573}\)
B chia hết cho 9
=>\(3+x+5+7+3⋮9\)
=>\(x+18⋮9\)
=>\(x\in\left\{0;9\right\}\)
10 tháng 12 2023
Bài 5:
Vì số bút chì khi đem chia 5 hoặc 3 thì vừa hết số bút chì sẽ vừa chia hết cho 5; vừa chia hết cho 3
=>Số bút chì sẽ chia hết cho 15
mà số bút chì có nhiều hơn 20 chiếc và ít hơn 35 chiếc
nên số bút chì là 30 chiếc
24 tháng 10 2023
Vì 40XY chia hết cho 2 và 5 nên 40XY sẽ có tận cùng là 0
=> Y = 0
Ta có 40X0 xhia hết cho 3
Để 40X0 chia hết cho 3 thì 4 + 0 + X + 0 chia hết cho 3
4 + X chia hết cho 3
=> X = { 2 , 5 , 8 }
Vậy X = { 2 , 5 , 8 } , Y = 0
Đây ạ!
VD
4 tháng 4 2018
Để 3a2b chia hết cho 2 và 5 => b=0
Ta có số: 3a20
Để 3a20 chia hết cho 3 => (3+a+2+0) chia hết cho 3
=> (5+a) chia hết cho 3, mà a là chữ số
=> 5+a=9
=> a=4
Vậy a=4, b=0
CM
12 tháng 6 2019
a) Vì A chia hết cho 2 nên chữ số cuối cùng phải là số chẵn.
Từ đó *ϵ{0;2;4;6;8}.
b) Vì A chia hết cho 5 nên chữ số cuối cùng phải là 0 hoặc 5.
Từ đó * ϵ{0;5}.
c) Vì A chia hết cho cả 2 và 5 nên chữ số cùng cuối cùng phải là 0.
Từ đó *ϵ {0}
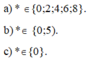
3744* Chia hết cho cả 2 và 5
=> * phải là 0
+) Xét tổng : 3 + 7 + 4 + 4 + 0 =18 chia hết cho 3
Vậy với * =0 thì số đã cho chia hết cho cả 2 ; 3 ; 5