Giải tam giác ABC vuông tại A biết ^C = 32 độ . SABC=80cm2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Ta có:
\(\widehat{B}=180^o-90^o-42^o=48^o\)
Xét tam giác ABC vuông tại A ta có:
\(cosB=\dfrac{AB}{BM}\Rightarrow cos48^o=\dfrac{6}{BM}\)
\(\Rightarrow BM=\dfrac{6}{cos48^o}\approx9\left(cm\right)\)
Mà: \(sinB=\dfrac{AM}{BM}\Rightarrow sin48^o=\dfrac{AM}{9}\)
\(\Rightarrow AM=9\cdot sin48^o\approx6,7\left(cm\right)\)

a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\widehat{ABC}=\widehat{HAC}\) do cùng phụ với góc BAH )
suy ra: \(\Delta ABC~\Delta HAC\)
b) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Áp dụng hệ thức lượng ta có:
\(AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8\)cm
\(CH=\frac{AC^2}{BC}=\frac{8^2}{10}=6,4\)cm
\(BH=BC-HC=10-6,4=3,6\)cm

Ta có : \(sinC=\frac{AB}{BC}=\frac{1}{2}\) nên \(BC=2AB=6\)
Suy ra , \(AC=\sqrt{BC^2-AB^2}=3\sqrt{3}\) và góc \(B=60^0\)
****
xét tam giác vuông ABC:
góc A+góc B+góc c=180 độ
90 độ+góc B+30 độ=180 độ
120 độ+góc B=180 độ
góc B=180-120
góc B=60 độ
tick nha

Ta co tinh chat canh doi dien voi goc 30do thi =1/2 canh huyen.o bai nay thi ta giai nhu sau.goi BC=a=>AB=a/2.ap dung PYTAGO =>(a/2)^2+100=a^2=>a= 11,55

a: \(\widehat{B}=60^0\)
AB=8cm
\(AC=4\sqrt{3}\left(cm\right)\)

Ta có
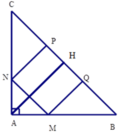
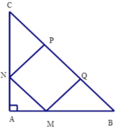
Kẻ AH ⊥ BC => H là trung điểm cạnh BC (vì tam giác ABC vuông cân tại A)
Khi đó AH là đường trung tuyến nên AH = B C 2 (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
Xét tam giác vuông CNP có C ^ = 450 (do tam giác ABC vuông cân) nên tam giác CNP vuông cân tại P
Suy ra CP =PN = 22cm
Tương tự ta có ΔQMB vuông cân tại Q => QM = QB = 22cm
Từ đó BC = PC + PQ + QB = 22 + 22 + 22 = 66cm
Mà AH = B C 2 (cmt) => AH = 66 2 = 33cm
Từ đó SABC = 1 2 AH.BC = 1 2 .33.66 = 1089 cm2
Đáp án cần chọn là: A
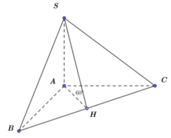
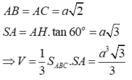
Trước tiên dễ dàng tính được \(\widehat{B}=58^o\)
Tam giác ABC vuông tại A nên \(\left\{{}\begin{matrix}AB=AC.tgC\\S_{ABC}=\dfrac{1}{2}AB.AC\end{matrix}\right.\)
Mà \(\widehat{C}=32^o;S_{ABC}=80cm^2\) nên ta có \(\left\{{}\begin{matrix}AB=AC.tg32^o\\\dfrac{1}{2}AB.AC=80\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=AC.tg32^o\\AB.AC=160\end{matrix}\right.\)
Từ 2 điều này, ta có \(AC.tg32^o.AC=160\Leftrightarrow AC^2=\dfrac{160}{tg32^o}\Leftrightarrow AC=\sqrt{\dfrac{160}{tg32^o}}\) \(\approx16\left(cm\right)\)
Từ đó ta có \(AB=\dfrac{160}{AC}=\dfrac{160}{\sqrt{\dfrac{160}{tg32^o}}}\approx10\left(cm\right)\)
Cuối cùng, ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{160}{\sqrt{\dfrac{160}{tg32^o}}}\right)^2+\left(\sqrt{\dfrac{160}{tg32^o}}\right)^2}\) \(\approx18,869\left(cm\right)\)