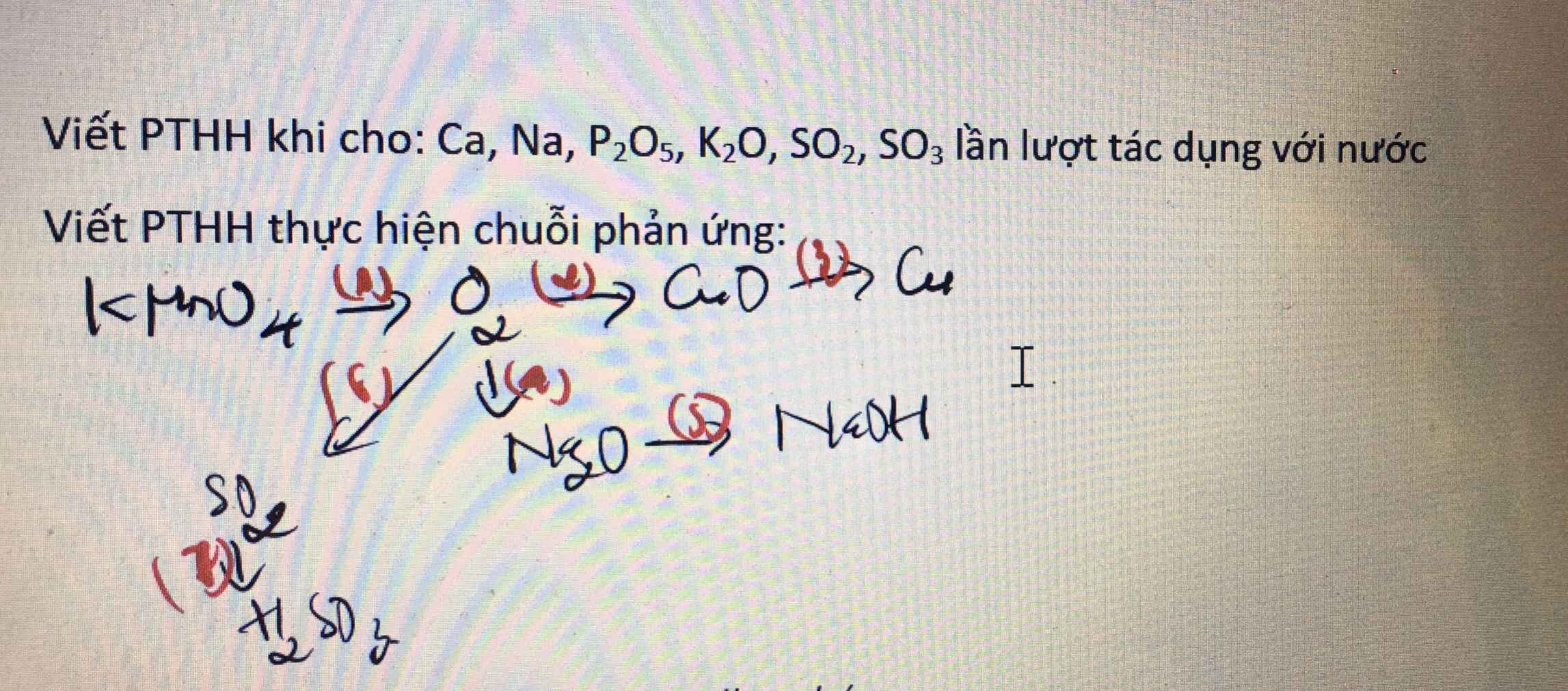Chữa giúp mình bài này với 🥺 giải thích thêm càng tốt ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LH
0
Những câu hỏi liên quan
VT
1
3 tháng 2 2023
a: Xét ΔBAC có BI/BA=BE/BC
nên EI//AC và EI=1/2AC
=>EI vuông góc AB
DE vuông góc AB tại trung điểm của DE
=>D đối xứng E qua AB
b: Xét tứ giác DECA co
DE//CA
DE=CA(=2EI)
Do đó: DECA là hình bình hành
c: Xét tứ giác ADBE có
I là trung điểm chung của AB và DE
EA=EB
=>ADBE là hình thoi
e: Để ADBE là hình vuông thì góc AEB=90 độ
=>góc ABC=45 độ
TM
3 tháng 2 2023
Bạn tự vẽ hình nhé.
a) Do \(E\) đối xứng với \(D\) qua \(I\), do đó \(I\) là trung điểm của \(DE\) hay \(ID=IE\).
Ta cũng có : \(E\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AB\) ⇒ \(IE\) là đường trung bình của \(\Delta ABC\) ⇒ \(IE // AC\). Lại có : \(AB\perp AC\) (giả thiết), vì vậy, \(IE\perp AB\).
Từ đó, suy ra \(AB\) là đường trung trực của \(DE\) hay \(D\) đối xứng với \(E\) qua \(AB\) (điều phải chứng minh).
b) Do \(IE\) là đường trung bình của \(\Delta ABC\) (chứng minh trên) nên \(IE=\dfrac{1}{2}AC\) và \(IE//AC\). Mặt khác, \(IE=\dfrac{1}{2}DE\). Suy ra được \(\dfrac{1}{2}AC=\dfrac{1}{2}DE\) hay \(AC=DE\). Suy ra, \(ADEC\) là hình bình hành (điều phải chứng minh).
c) Do \(I\) là trung điểm của \(DE\) (chứng minh trên) và của \(AB\) (giả thiết), suy ra \(ADBE\) là hình bình hành. Lại có \(AB\perp DE\) (do \(AB\) là đường trung trực của \(DE\) (chứng minh trên)). Suy ra, \(ADBE\) là hình thoi.
Do \(ADBE\) là hình thoi nên \(AE=EB=BD=DA=10(cm)\). Do đó, chu vi của hình thoi \(ADBE\) là \(C=AE+EB+BD+DA=4AE=4.10=40\left(cm\right)\).
d) Để hình thoi \(ADBE\) là hình vuông thì \(\hat{E}=90^o\) hay \(AE\) là đường cao của \(\Delta ABC\). Mà \(AE\) lại là đường trung tuyến của \(\Delta ABC\) (do \(E\) là trung điểm của \(BC\)). Để điều đó xảy ra thì \(\Delta ABC\) phải thêm điều kiện cân tại \(A\).
PT
2
TL
Trịnh Long
CTVVIP
30 tháng 5 2022
Bài 4
a, Số nu của gen là 90 x 20 = 1800 ( nu )
=> Chiều dài của gen \(\dfrac{1800}{2}.3,4=3060\left(A^O\right)\)
b,
Số nu của cả gen A=T=1800.20% = 360 (nu)
G=X=1800.30% = 540(nu)
Số nu từng mạch :
A1 = T2 = 15% . 900 = 135 ( nu )
T1 = A2 = 360 - 135 = 225 ( nu )
G1 = X2 = 540 - X1 = 540 - 360 = 180 ( nu )
X1 = G2 = 40% . 900 = 360 ( nu )
TL
Trịnh Long
CTVVIP
30 tháng 5 2022
Bài 5
Ta có : \(\left\{{}\begin{matrix}H=2A+3G=N+G=3900\\G=900\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=T=600\left(nu\right)\\G=X=900\left(nu\right)\\N=3000,N1=N2=1500\left(nu\right)\end{matrix}\right.\)
A1 = T2 = 30%.1500= 450 (nu)
T1 = A2 = 600 - 450 = 150 (nu)
G1 = X2 = 10%.1500 = 150 ( nu )
G2 = X1 = 900 - 150 = 750 (nu)
BC
2
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
HP
11 tháng 4 2021
7.
Phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) với tâm \(I=\left(a;b\right)\), bán kính \(R\)
\(\Rightarrow\) Tâm đường tròn \(\left(x-1\right)^2+\left(y+2\right)^2=4\) có tọa độ \(\left(1;-2\right)\)
Kết luận: Tâm đường tròn có tọa độ \(\left(1;-2\right)\).
VY
2
3 tháng 4 2022
1.
\(Ca+2H_2O\rightarrow Ca\left(OH\right)_2+H_2\)
\(2Na+2H_2O\rightarrow2NaOH+H_2\)
\(P_2O_5+3H_2O\rightarrow2H_3PO_4\)
\(K_2O+H_2O\rightarrow2KOH\)
\(SO_2+H_2O\rightarrow H_2SO_3\)
\(SO_3+H_2O\rightarrow H_2SO_4\)
2.
(1)\(2KMnO_4\rightarrow\left(t^o\right)K_2MnO_4+MnO_2+O_2\)
(2)\(2Cu+O_2\rightarrow\left(t^o\right)2CuO\)
(3)\(CuO+H_2\rightarrow\left(t^o\right)Cu+H_2O\)
(4)\(4Na+O_2\rightarrow\left(t^o\right)2Na_2O\)
(5)\(Na_2O+H_2O\rightarrow2NaOH\)
(6)\(S+O_2\rightarrow\left(t^o\right)SO_2\)
(7)\(SO_2+H_2O\rightarrow H_2SO_3\)
3 tháng 4 2022
(1) 2KMnO4 --to--> K2MnO4 + MnO2 + O2
(2) 2Cu + O2 --to--> 2CuO
(3) CuO + CO --to--> Cu + CO2
(4) 4Na + O2 --to--> 2Na2O
(5) Na2O + H2O ---> 2NaOH
(6) S + O2 --to--> SO2
(7) SO2 + H2O ---> H2SO3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
LN
1
TP
28 tháng 12 2021
Chọn D. Cồn là 1 hỗn hợp vì trong cồn 70 độ gồm C2H5OH và nước
11 tháng 2 2020
\(-\left(-220\right)-78-220-\left(-78\right)-23=220-78-220+78-23\)
\(=\left(220-220\right)+\left(-78+78\right)-23\)
\(=0-23\)
\(=-23\)