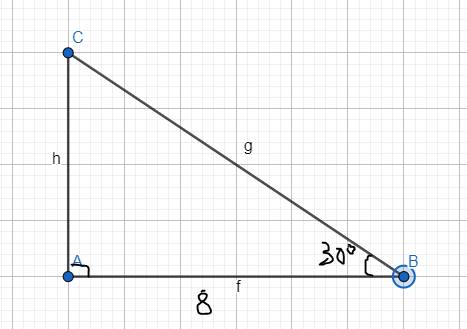
Cho hình tam giác ABC có gióc A=90 độ (AB<AC), kẻ AH vuông góc với BC (H thuộc BC). Trên BC lấy I sao cho HI=HB. Trên tia đối của tia HA lấy K sao cho HK=HA
a) Chứng minh tam giác ABH= tam giác KIH
b) Chứng minh AB song song với KI
c) Vẽ IE vuông góc với AC tại E. Chứng minh K, I, E thẳng hàng
d) Trên tia đối của tia IA lấy D sao cho ID=IA. Chứng minh góc IKD= góc IDK